MathProf - Ebene - Parameterform - Parametergleichung - Gerade
Fachthema: Ebene in Punktrichtungsform
MathProf - Vektoralgebra - Eine Software, welche als Begleiter beim Maschinenbau-Studium oder Elektrotechnik-Studium zur Lösung anspruchsvoller Aufgaben sowie zur Erlangung tiefergreifenden Fachwissens der Mathematik eingesetzt werden kann. Auch dient es zum Lösen verschiedenster Aufgaben und zur Erkundung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Visualisierungen.
Online-Hilfe
für das Modul Analytische Geometrie (Vektorgeometrie)
zur Praktizierung von Untersuchungen mit Ebenen im 3D-Koordinatensystem, beschrieben durch eine Ebenengleichung in Punkt-Richtungs-Form (Punktrichtungsgleichung einer Ebene bzw. Parametergleichung einer Ebene) sowie mit Geraden und Punkten im Raum.
Dieses Unterprogramm ermöglicht unter anderem die Durchführung der Analyse der Lagebeziehung zwischen einer auf diese Weise definierten Ebene und einer Gerade. Auch das Berechnen des Durchstoßpunkts Gerade-Ebene sowie von einem evtl. vorhandenen Schnittpunkt der festgelegten Gerade und der Ebene im Raum kann vollzogen werden.
Zudem erfolgt das Berechnen und die Darstellung von Ortsvektor (Stützvektor), Richtungsvektor und Normalenvektor (nach dessen Normierung) der definierten Ebene sowie die Berechnung der Spurpunkte dieser.
Darüber hinaus kann der implementierte Rechner den Abstand zwischen einem Punkt und einer Ebene dieser Art ermitteln (Abstand Punkt-Ebene). Der ggf. vorhandene Schnittpunkt einer derartig beschriebenen Ebene und einer Gerade wird ebenfalls berechnet und der Winkel zwischen Ebene und Gerade wird ausgegeben.
Der implementierte 3D-Plotter bietet ein frei bewegbares und drehbares, dreidimensionales Koordinatensystem und ermöglicht die Durchführung interaktiver Analysen bzgl. Sachverhalten und relevanter Zusammenhänge zu diesem Fachthema. Auch die Ausführung verschiedener 3D-Animationen mit Gebilden dieser Art kann veranlasst werden.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind eingebunden.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Ebenen - 3D - Geraden - Vektorielle Darstellung von Ebenen - Analytische Geometrie - Ebenengleichungen - Punkt-Richtungs-Form - Ebene in Parameterform - Ebenengleichung in Parameterform - Ebene grafisch darstellen - Parametergleichung einer Ebene - Parameterdarstellung einer Ebene - Ebene im Raum - Parameterform einer Ebene - Vektorielle Parametergleichung - Schnittpunkt von Gerade und Ebene - Lagebeziehung Ebene-Punkt - Abstand Punkt-Ebene - Schnitt einer Ebene und einer Gerade - Vektoren - Spannvektoren - Dreidimensional - 3D - Rechner - Graph - Grafisch - Herleitung - Beweis - Bild - Plotter - Darstellung - Präsentation - Bedeutung - Was ist - Wie - Weshalb - Was bedeutet - Welche - Welcher - Welches - Wodurch - Erklärung - Einfach erklärt - Einführung - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Mathe - Mathematik - Begriff - Begriffe - Definition - Berechnung - Darstellen - Untersuchen - Berechnen - Plotten - Zeichnen - Untersuchung - Spurpunkte einer Ebene - Normalenvektor - Normalenvektor einer Ebene - Abstand - Abstandsbestimmung - Darstellung einer Ebene - Durchstoßpunkt - Lagebeziehung von Ebene und Gerade - Abstand zwischen Punkt und Ebene - Punktrichtungsgleichung einer Ebene - Abstand einer Ebene vom Ursprung - Abstandsberechnung Punkt Ebene - Punkt - Punktprobe - Vektorielle Parametergleichung einer Ebene - Gegenseitige Lage von Ebene und Gerade - Ebenen im Raum - Aufpunkt - Stützvektor - Abstandsberechnung - Parameter - Ebene plotten - Ebene zeichnen - Punktprobe mit einer Ebene - Ebene und Vektoren - Richtungsvektor einer Ebene - Ortsvektor einer Ebene - Winkel zwischen Gerade und Ebene - Spurpunkte einer Ebene - Durchstoßpunkt Gerade-Ebene - Umwandlung von Parameterform in Normalenform - Umwandlung - Schneiden - Parallel - Lage - Gegenseitige Lage - Normalabstand - N-Vektor - Punkt - Ebene - Senkrecht - Senkrecht zueinander - Schnittpunkte mit Koordinatenachsen - Darstellungsarten - Darstellungsformen - Formel - Spurpunkte - R3 - Gemeinsame Punkte - Schnittwinkel von Ebene und Gerade |
Ebene im Raum in Punkt-Richtungs-Form - Gerade - Punkt
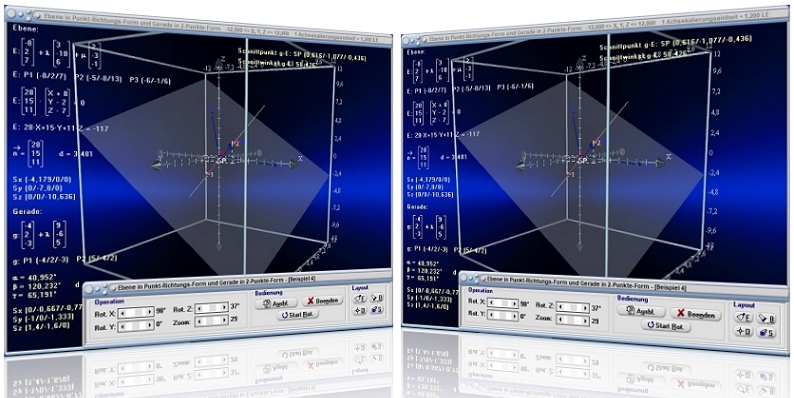
Modul Ebene in Punkt-Richtungsform
Das Unterprogramm [Vektoralgebra] - Ebene in P-R-Form ermöglicht die Durchführung von Untersuchungen mit Ebenengleichungen in Punkt-Richtungs-Form (Parameterform - Parametergleichung - Parameterdarstellung), Geraden und Punkten im Raum.
Die Anwendungsmöglichkeiten dieses Unterprogramms sind:
- Analyse der Eigenschaften einer Ebene in Punkt-Richtungs-Form (Parameterform - Parametergleichung)
- Darstellung einer Ebene in Punkt-Richtungs-Form (sowie eines Punktes, oder einer Geraden)
- Abstand Punkt - Ebene: Berechnung des Abstands eines Punktes von einer Ebene in Punkt-Richtungs-Form (Parameterform)
- Ermittlung des Schnittpunkts und des Schnittwinkels einer Ebene in Punkt-Richtungs-Form (Parameterform) und einer Geraden
- Ermittlung des Abstands einer Geraden zu einer Ebene in Punkt-Richtungs-Form (Parameterform)
- Darstellung der Lotgerade durch einen Punkt auf eine Ebene in Punkt-Richtungs-Form (Parameterform)
Definitionsformen von Ebenen und Geraden (Ebenengleichung - Geradengleichung - Formel)
Mögliche Definitionsformen von Ebenen und Geraden in diesem Unterprogramm sind:
1. Parameterdarstellung (Parametergleichung) einer Ebene in Punkt-Richtungs-Form (r1 ist Stützvektor gebildet aus Aufpunkt, a und b sind Spannvektoren):
2. Parameterdarstellung (Parametergleichung) einer Geraden in Punkt-Richtungs-Form:
3. Darstellung einer Geraden in Zwei-Punkte-Form:
Grundlegendes zu Gerade und Ebene
Grundlegendes:
Ebene: Bei einer Ebenengleichung handelt es sich um eine Gleichung, die eine Ebene im dreidimensionalen Raum charakerisiert. Eine Ebene besteht in einem kartesischen Koordinatensystem aus den Punkten, deren Koordinatenvektoren diese Ebenengleichung erfüllen. Ebenen können unter anderem in einer der folgenden Arten in Form einer Gleichung definiert werden: Punkt-Richtungs-Form (Parameterform), Normalenform oder Koordinatenform.
Normalenvektor: Ein Normalenvektor ist ein Vektor der orthogonal auf einer Geraden, Kurve, einer gekrümmten Fläche oder Ebene steht. Eine Gerade die diesen Vektor als Richtungsvektor besitzt wird als Normale bezeichnet. Ein Normalenvektor der Länge 1 wird als Einheitsnormale bezeichnet.
Stützvektor einer Ebene: Der Stützvektor einer Ebene (oder einer Gerade) im Raum ist derjenige Vektor, dem ein skalares Vielfaches seines Richtungsvektors hinzuaddiert wird. Er ist der Ortsvektor des Punkts der Ebene oder Gerade von welchem aus der Stützvektor aufgesetzt wird.
Spannvektoren: Bei Spannvektoren handelt es sich um Vektoren, die sich durch Parallelverschiebung in die Ebene in Form von Pfeilen darstellen lassen. Sie dürfen nicht parallel verlaufen (oder aufeinanderliegen).
Aufpunkt: Als Aufpunkt wird ein bereits bekannter Punkt einer Ebene oder einer Gerade bezeichnet, mit Hilfe dessen es möglich ist, eine Gleichung für diese Ebene bzw. Gerade aufzustellen.
Für eine Gerade und eine Ebene gilt:
- Eine Gerade liegt in einer Ebene, wenn sie mit ihr zwei gemeinsame Punkte besitzt
- Eine Gerade liegt parallel zu einer Ebene, wenn sie mit ihr keinen gemeinsamen Punkt besitzt, oder ganz in der Ebene liegt
- Eine Gerade schneidet eine Ebene, wenn sie mit ihr exakt einen gemeinsamen Punkt besitzt. Dieser gemeinsame Punkt trägt die Bezeichnung Schnittpunkt, Durchstoßpunkt oder Spurpunkt
- Eine Gerade steht senkrecht (orthogonal) auf einer Ebene, wenn sie wenigstens mit zwei voneinander verschiedenen Geraden, welche in der Ebene liegen und sich unterscheiden, einen rechten Winkel einschließt
Lage einer Ebene und einer Gerade
Die Lage einer Ebene im Raum ist eindeutig bestimmt durch:
- zwei sich schneidende Geraden g1 und g2
- drei, nicht auf einer Gerade liegende Punkte
- zwei zueinander parallel liegende Geraden g1 und g2
- einen Punkt P, einen Richtungsvektor sowie einen orthogonal auf dieser stehenden Normalenvektor
- eine Gerade sowie einen nicht auf dieser liegenden Punkt
Mögliche Lagen, die eine Gerade g und eine Ebene E zueinander besitzen können:
- Gerade g liegt in Ebene E
- Gerade g und Ebene E liegen parallel zueinander
- Gerade g und Ebene E schneiden sich in einem Punkt (Schnittpunkt)
Zusammenhänge und Formeln
Formeln zu diesem Fachthema, die für eine Ebene in Normalenform sowie für eine Gerade in Punkt-Richtungs-Form anwendbar sind, sind nachfolgend gezeigt.
1. Abstand Punkt - Ebene:
Für den Abstand eines Punktes Q von einer Ebene in Normalen-Form gilt:
rQ: Ortsvektor des Punktes Q
2. Abstand einer Geraden in Punkt-Richtungs-Form von einer Ebene in Normalen-Form:
Für den Abstand einer Gerade in Punkt-Richtungsform von einer Ebene in Normalen-Form gilt:
Gleichung der Gerade:
Gleichung der Ebene:
Der Abstand der Gerade von der Ebene beträgt:
3. Abstand zweier paralleler Ebenen:
Definitionsform der Ebene 1:
Definitionsform der Ebene 2:
Der Abstand der Ebene1 von der Ebene2 kann wie folgt berechnet werden:
4. Schnittpunkt Ebene - Gerade:
Definitionsform der Gerade:
Definitionsform der Ebene (Normalenfom):
Der Schnittpunkt der Ebene und der Gerade kann wie folgt berechnet werden:
Für den Schnittwinkel einer Ebene in Normalenform und einer Gerade in Punkt-Richtungsform gilt:
Zur Verwendung o.a. Vektorgleichungen sind die Darstellungsformen der Ebene in Normalenform und die der Gerade in Punkt-Richtungs-Form zu bringen.
Bedeutung der im Programm verwendeten Bezeichnungskürzel
Die Bedeutungen der im Programm verwendeten Bezeichungskürzel sind folgende:
| E,E1,E2: | Ebene in 3-Punkte-, Punkt-Richtungs-, Normalen-, sowie Koordinatenform |
| d: | Abstand einer Ebene vom Koordinatenursprung, Abstand einer Geraden vom Koordinatenursprung |
| n,n1,n2: | Normalenvektor einer Ebene |
| Sx,Sy,Sz: | Spurpunkte einer Ebene, bzw. Gerade |
| SP: | Schnittpunkt einer Ebene und einer Gerade, Schnittpunkt zweier Geraden |
| SW: | Schnittwinkel zweier Ebenen, zweier Geraden, einer Geraden und einer Ebene |
| g,g1,g2: | Gerade in 2-Punkte- oder Punkt-Richtungs-Form |
| α,β,γ: | Neigungswinkel einer Geraden bzgl. entspr. Achsen |
| r,r1,r2: | Ortsvektor einer Geraden, oder einer Ebene |
| a,b: | Richtungsvektor einer Geraden, oder einer Ebene (Spannvektor) |
| P,P1,P2,P3: | Punkte |
| λ;μ: | Parameterwerte für Richtungsvektoren einer Geraden, bzw. einer Ebene |
| g-E: | Gerade - Ebene |
| g1-g2: | Gerade 1 - Gerade 2 |
| E1-E2: | Ebene 1 - Ebene 2 |
Screenshots
Grafische Darstellung - Beispiel 1
Grafische Darstellung - Beispiel 2
Grafische Darstellung - Beispiel 3
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Darstellung einer Ebene in Punkt-Richtungs-Form
Um eine Ebene, welche in Punkt-Richtungs-Form definiert ist, darstellen zu lassen, führen Sie Folgendes aus:
- Aktivieren Sie Kontrollschalter Automatisch oder Statisch.
- Aktivieren Sie den Kontrollschalter Ebene.
- Geben Sie die Koeffizientenwerte der Vektoren der Ebene in die dafür vorgesehenen Felder r, a und b ein.
- Bedienen Sie die Schaltfläche Darstellen.
Eigenschaftsanalyse einer Ebene in Punkt-Richtungs-Form (Parameterform)
Die Untersuchung einer Ebene auf deren Eigenschaften können Sie durchführen, indem Sie wie nachfolgend beschrieben
vorgehen:
- Aktivieren Sie den Kontrollschalter Ebene.
- Geben Sie die Koeffizientenwerte der Vektoren der Ebene in die hierfür vorgesehenen Felder r, a und b ein.
- Bedienen Sie die Schaltfläche Berechnen.
Nachfolgend aufgeführte Details einer Ebene in Punkt-Richtungs-Form (Parameterform) werden bei Durchführung einer Eigenschaftsanalyse errechnet:
- Abstand d der Ebene vom Koordinatenursprung
- Spurpunkte Sx,Sy,Sz (Durchstoßpunkte) der Ebene
- Normalenvektor n der Ebene
- Definition der Ebene in 3-Punkte-, Punkt-Richtungs-, Normalen-, sowie Koordinatenform
Abstand eines Punktes von einer Ebene in Punkt-Richtungs-Form (Parameterform - Parameterdarstellung)
Berechnung und grafische Darstellung
Um den Abstand eines Punktes von einer Ebene ermitteln zu lassen, sollten Sie Folgendes ausführen:
- Aktivieren Sie Kontrollschalter Automatisch oder Statisch.
- Aktivieren Sie den Kontrollschalter Ebene und Punkt.
- Geben Sie die Koeffizientenwerte der Vektoren der Ebene in die hierfür vorgesehenen Felder r, a und b ein.
- Bedienen Sie die Schaltfläche Berechnen und legen Sie die Koordinatenwerte des Punktes P in den zur Verfügung stehenden Eingabefeldern (x,y,z) des Unterformulars fest.
- Bedienen Sie die im Unterformular zur Verfügung stehende Schaltfläche Berechnen.
- Möchten Sie sich die Lage des Punktes und der Ebene grafisch veranschaulichen, so bedienen Sie die im Unterformular zur Verfügung stehende Schaltfläche Darstellen.
Soll bei Ausgabe der Darstellung eine Strecke eingezeichnet werden, die vertikal auf der Ebene steht und durch Punkt P verläuft, so aktivieren Sie das Kontrollkästchen Abstandslinie.
Schnittpunkt, Schnittwinkel und Abstand einer Ebene in Punkt-Richtungs-Form (Parameterform) und einer Geraden
Berechnung und grafsiche Darstellung
Um Schnittpunkt, sowie Schnittwinkel einer Geraden und einer Ebene ermitteln zu lassen, sollten Sie Folgendes ausführen:
- Aktivieren Sie Kontrollschalter Automatisch oder Statisch.
- Möchten Sie die Lagen einer Ebene in Punkt-Richtungs-Form und einer Geraden in 2-Punkte-Form analysieren, so aktivieren Sie den Kontrollschalter Ebene und Gerade in 2-P-Form. Um die Lagen einer Ebene in Punkt-Richtungs-Form und einer Geraden in Punkt-Richtungs-Form zu untersuchen, aktivieren Sie den Kontrollschalter Ebene und Gerade in P-R-Form.
- Geben Sie die Koeffizientenwerte der Vektoren der Ebene in die dafür vorgesehenen Felder r, a und b im Hauptformular ein.
- Bedienen Sie die Schaltfläche Berechnen.
- Geben Sie die Koeffizientenwerte, bzw. Punktkoordinaten der Vektoren der Geraden in die dafür vorgesehenen Felder im Unterformular ein.
- Bedienen Sie die im Unterformular zur Verfügung stehende Schaltfläche Berechnen.
- Möchten Sie sich die Lagen der Gerade sowie der Ebene grafisch veranschaulichen, so bedienen Sie die im Unterformular zur Verfügung stehende Schaltfläche Darstellen.
Liegen Gerade und Ebene parallel, so ermittelt das Programm deren Abstand.
Hinweis:
Benötigen Sie Detailinformationen bezüglich der Eigenschaften einer Geraden mit welcher Berechnungen durchzuführen sind, so wählen Sie auf dem Eingabeformular zur Definition der Geraden den Menüpunkt Details.
Darstellungsbereich
Bei Ausgabe der Darstellung ermöglicht das Programm die Bemessung des Darstellungsbereichs auf eine der folgenden Arten und Weisen:
-
Automatisch
-
Statisch
-
Automatisch:
Wird die Einstellung Automatisch durch die Aktivierung des dafür vorgesehenen Kontrollschalters gewählt, so ermittelt das Programm alle zur vollständigen Darstellung des Gebildes erforderlichen x-, y- und z-Koordinatenwerte automatisch und bemisst den Darstellungsbereich dementsprechend.
-
Statisch:
Wird der Kontrollschalter Statisch aktiviert, so verwendet das Programm bei Aufruf der Darstellung den unter Abs. Bereich voreingestellten Darstellungsbereich und beschneidet Gebilde an Stellen, die außerhalb dessen liegen. Diesen Bereich können Sie bei Ausgabe der Darstellung verändern, indem Sie den auf dem Bedienformular zur Verfügung stehenden Rollbalken Bereich positionieren. Der maximal einstellbare Wert entspricht dem Doppelten des unter Abs. Bereich auf dem Hauptformular des Unterprogramms vorgegebenen Werts.
Grafische Darstellung - Optionen
Im Formularbereich Darstellung - Optionen können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende Einstellungen vornehmen, die bei Ausgabe der grafischen Darstellung der Zusammenhänge wirksam werden:
- Geradenvektoren: Darstellung des Orts- und des Richtungsvektors der Geraden ein-/ausschalten
- N-Vektor d. Ebene: Darstellung des Normalenvektors der Ebene ein-/ausschalten
- Ebenenvektoren: Darstellung des Ortsvektors und der Richtungsvektoren der Ebene ein-/ausschalten
- Beschriftung: Beschriftung dargestellter Vektoren und Punkte ein-/ausschalten
- Abstandslinie: Darstellung der vertikalen Abstandslinie zwischen Ebene und Gerade ein-/ausschalten
- Hilfslinien: Darstellung von Hilfslinien der Gerade ein-/ausschalten
- Textausgabe: Anzeige ermittelter Ergebnisse bei Ausgabe der Darstellung ein-/ausschalten
Allgemein
Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.
Weitere Themenbereiche
Gerade in Punkt-Richtungs-Form (3D)
Ebene in Koordinaten-Form (3D)
Beispiele
Beispiel 1 - Eigenschaften der Ebene in Punkt-Richtungs-Form (Parameterform - Parameterdarstellung):
Es gilt, sich die Eigenschaften einer Ebene ausgeben zu lassen, welche durch nachfolgend gezeigte Gleichung beschrieben wird:
Vorgehensweise und Lösung:
Nach einer Aktivierung des Kontrollschalters Ebene und einer Eingabe der Koeffizientenwerte zur Definition der Ebene E in Punkt-Richtungs-Form, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse:
Die Gleichung der definierten Ebene E in vektorieller Schreibweise in Normalen-Form lautet:
Drei Punkte, die auf der Ebene E liegen:
P1 (4 / 2 / -7)
P2 (5 / 5 / -1)
P3 (-1 / 3 / -8)
Die Gleichung der definierten Ebene E in Koordinaten-Form lautet:
E: -9·X - 29·Y + 16·Z = -206
Der Abstand der Ebene E vom Koordinatenursprung beträgt d = 6,002.
Die Spurpunkte der Ebene E sind:
Sx (22,889 / 0 / 0)
Sy (0 / 7,103 / 0)
Sz (0 / 0 / -12,875)
Der Normalenvektor der Ebene E lautet:
Der Betrag des Normalenvektors der Ebene besitzt den Wert 34,322.
Beispiel 2 - Abstand eines Punkts von einer Ebene in Punkt-Richtungs-Form (Parameterform - Parameterdarstellung):
Es gilt, den Abstand des Punktes P (2 / 2 / -2) von einer Ebene E in Punkt-Richtungs-Form ermitteln zu lassen, welche durch nachfolgend gezeigte Gleichung beschrieben wird:
Vorgehensweise und Lösung:
Nach einer Aktivierung des Kontrollschalters Ebene und Punkt, der Eingabe der Koeffizientenwerte der Ebene E in Punkt-Richtungs-Form und einer Bedienung der Schaltfläche Berechnen, sowie der Eingabe der Koordinatenwerte des Punkts im Unterformular, ermittelt das Programm nach einem Klick auf die dortige Schaltfläche Berechnen:
Der Abstand des Punktes P von der Ebene beträgt d = 6,387.
Beispiel 3 - Ebene in Punkt-Richtungs-Form (Parameterform - Parameterdarstellung) - Gerade in 2-Punkte-Form:
Es ist eine Analyse bzgl. der Lagen einer Ebene E in Punkt-Richtungs-Form
und einer Geraden, welche durch die beiden Punkte P1 (2 / 1 / 8) und P2 (-2 / 3 / -5) verläuft, durchzuführen.
Vorgehensweise und Lösung:
Nach einer Aktivierung des Kontrollschalters Ebene und Gerade in 2-P-Form, der Eingabe der Koeffizientenwerte der Ebene E in Punkt-Richtungs-Form einer Bedienung der Schaltfläche Berechnen, sowie der Eingabe der Koordinatenwerte der Punkte P1 und P2 im Unterformular zur Definition der Gerade g, gibt das Programm nach einem Klick auf die dortige Schaltfläche Berechnen aus:
Ebene und Gerade schneiden sich in Punkt SP (5,411 / -0,705 / 19,084).
Der Schnittwinkel von Ebene und Gerade beträgt 12,206°.
Nach einer Wahl des Menüpunkts Details im Unterformular zur Definition der Geraden erhalten Sie darüber hinaus folgende Informationen bzgl. der Eigenschaften, der durch die beiden Punkte P1 und P2 definierten Gerade.
Die Gleichung der Geraden g in vektorieller Schreibweise in Punkt-Richtungs-Form lautet:
Die Richtungswinkel der Gerade g sind:
α = 106,915°
β = 81,635°
γ = 161,016°
Der Abstand der Geraden g vom Koordinatenursprung beträgt d = 2,231.
Die Spurpunkte der Gerade g sind:
Sx (0 / 2 / 1,5)
Sy (4 / 0 / 14,5)
Sz (-0,462 / 2,231 / 0)
Die Länge der Strecke zwischen den Geradenpunkten P1 und P2 beträgt 13,748.
Grafische Darstellung - Beispiel 4
Grafische Darstellung - Beispiel 5
Grafische Darstellung - Beispiel 6
Grafische Darstellung - Beispiel 7
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Ebenengleichung
Wikipedia - Parameterform
Wikipedia - Schnittpunkt einer Gerade und einer Ebene
Gerade und Vektoren - Vektorielle Linearkombination - Vektorielles Teilverhältnis - Vektoraddition in der Ebene - Resultierende - Komponentendarstellung (3D) - Vektorprodukt (3D) - Skalarprodukt (3D) - Spatprodukt (3D) - Vektorprojektion (3D) - Tripelprodukt (3D) - Numerische Vektoraddition im Raum - Grafische Vektoraddition im Raum (3D) - Gerade in Punkt-Richtungs-Form (3D) - Gerade in 2-Punkte-Form (3D) - Ebene in 3-Punkte-Form (3D) - Ebene in Normalen-Form (3D) - Ebene in Koordinaten-Form (3D) - Zwei Ebenen (3D) - Kugel - Gerade (3D) - Kugel - Ebene - Punkt (3D) - Kugel - Kugel (3D)
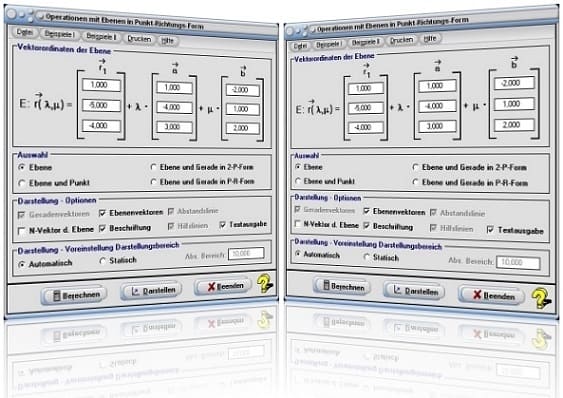
Startfenster des Unterprogramms Ebene in Punkt-Richtungsform
MathProf 5.0 - Startfenster des Unterprogramms Ebene in Koordinatenform
MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
