MathProf - Prisma - Pyramide - Kegel - Kugel - Keil - Pyramidenstumpf

 

Modul Eben- und krummflächig begrenzte Körper

---

 
Das Unterprogramm [Geometrie] - Eben- und krummflächig begrenzte Körper ermöglicht die Berechnung, sowie die dreidimensionale Darstellung verschiedener ebenflächig und krummflächig begrenzter mathematischer Raumkörper (Raumgebilde) aus dem Bereich der räumlichen Geometrie.

 

 

Ein Körper ist die Menge aller Punkte, Geraden und Ebenen im dreidimensionalen Raum, die sich innerhalb eines vollständig abgeschlossenen Teils des Raumes befinden. Die Oberfläche eines Körpers ist die Summe aller seiner Begrenzungsflächen. Als Rauminhalt oder Volumen eines Körpers wird die Größe des Raums bezeichnet, welche von seinen Begrenzungsflächen eingeschlossen wird. Ebenflächig begrenzte Körper sind Körper, welche von ebenen Flächen begrenzt werden. Krummflächig begrenzte Körper werden ganz, oder teilweise von krummen Flächen begrenzt.  
 
Untersuchungen und Berechnungen können in diesem Modul mit nachfolgend aufgeführten Körpern durchgeführt werden:

• Regelmäßiges Prisma
• Senkrechter Zylinder (Kreiszylinder)
• Vierseitige Pyramide
• Senkrechter Kreiskegel (Kegel)
• Kugel
• Keil
• Obelisk
• Doppelpyramide
• Pyramidenstumpf
• Schiefes Prisma
• Schiefe Pyramide
• N-seitige Pyramide

 

 
Prismen: Ein Prisma ist ein Vielflach, dessen Oberfläche sich aus zwei kongruenten und parallel liegenden Vielecken zusammensetzt. Es besitzt ebenso viele vertikal angeordnete Parallelogramme als jedes seiner Vielecke Seiten besitzt. Gerades Prisma - Senkrechtes Prisma (gerade Prismen): Prismen heißen gerade, wenn ihre Seitenkanten vertikal auf deren Grundfläche stehen. Ist dies nicht der Fall, so heißt das Prisma schiefes Prisma (schräges Prisma). Ein Prisma wird als regelmäßig bezeichnet, wenn es senkrecht ist und als Grundfläche regelmäßige Vielecke besitzt.

Pyramiden: Eine Pyramide ist ein Vielflach, dessen Oberfläche sich aus einem Vieleck sowie ebenso vielen Dreiecken zusammensetzt. Das Dreieck wird als Grundfläche bezeichnet, die Dreiecke sind die Seitenfläche der Pyramide. Die Seiten der Grundfläche eines derartigen Gebildes werden als Grundkanten bezeichnet, alle anderen Seitenkanten. Der Abstand der Spitze der Pyramide von ihrer Grundfläche heißt Pyramidenhöhe. Das Volumen einer Pyramide wird mit dem Ausdruck Pyramidenvolumen beschrieben.

Pyramiden heißen regelmäßig, wenn ihre Grundfläche aus einem regelmäßigen Vieleck besteht und die Gerade, welche durch ihre Spitze und den Mittelpunkt ihrer Grundfläche verläuft, senkrecht steht. Pyramiden dieser Art tragen die Bezeichnung regelmäßige Pyramide. Als schiefe Pyramide wird eine Pyramide bezeichnet, wenn sich deren Spitze nicht senkrecht über dem Mittelpunkt der Grundfläche befindet, ansonsten heißt sie gerade Pyramide. Eine Pyramide dessen Grundfläche ein Dreieck ist, wird als dreiseitige Pyramide (Dreieckspyramide) bezeichnet. Besitzt sie ein Viereck als Grundfläche, so heißt sie vierseitige Pyramide. Eine n-seitige Pyramide wird sie genannt, wenn ein n-Eck seine Grundfläche bildet. Besitzt eine Pyramide einer rechteckige Grundfläche, so handelt es sich um eine rechteckige Pyramide.
 
Pyramidenstumpf: Der Pyramidenstumpf ist ein ebenflächig begrenzter Körper, dessen Grundfläche und Deckfläche parallel liegen. Seine verlängerten Seiten schneiden sich in einem Punkt der außerhalb dessen liegt. Er kann durch das Aufsetzen einer Ergänzungspyramide zu einer vollständigen Pyramide vervollständigt werden. Seine Mantelfläche bildet sich aus der Summe seiner Seitenflächen. Ein rechteckiger Pyramidenstumpf besitzt eine rechteckige Grundfläche und ein quadratischer Pyramidenstumpf verfügt über eine quadratische Grundfläche.

Prismatoid: Ein Prismatoid ist ein Vielflach (Polyeder), welches von zwei beliebigen, parallelen Vielecken sowie zudem von Dreiecken, von welchen jedes mit einem Vieleck eine gemeinsame Seite, mit dem anderen eine gemeinsame Ecke besitzt, begrenzt wird. Im Gegensatz zum Prisma müssen Deckfläche und Grundfläche nicht kongruent sein und können unterschiedliche Eckenzahlen besitzen.

Keile: Der Keil stellt eine Sonderform des Prismatoids dar. Er besitzt keine Deckfläche, sondern eine parallele, zur Basis verlaufende Gerade. Er ist ein geometrischer Körper, bei dem zwei Seitenflächen unter einem spitzen Winkel, dem Keilwinkel münden.
 
Obelisk: Ein ebenflächig begrenzter Körper, welcher sich aus rechteckigen, parallel liegenden Grundflächen und Deckflächen sowie aus trapezförmigen Seitenflächen zusammensetzt, wird als Obelisk bezeichnet.

Zusammengesetzte Körper: Als zusammengesetzter Körper wird ein geometrischer Körper bezeichnet, der aus mehreren einzelnen Teilkörpern besteht. Dessen Oberfläche bildet sich aus der Summe aller ihn begrenzenden Teilflächen. Sein Volumen entspricht der Summe der Volumina aller seiner einzelner Teilkörper. Seine Teilkörper können beispielsweise Quader, Pyramiden, Kegel, Prismen oder Zylinder sein.
 

 
Nachfolgend aufgeführt sind einige Formeln, welche zur Berechnung der Werte entsprechender Größen einiger Körper benötigt werden.

Kugel:

Durchmesser: d = 2·r
Oberfläche: A = 4·π·r²
Volumen: V = 4/3·π·r³

Mit:
r: Radius der Kugel
 
Zylinder:

Durchmesser: d = √ h² + ( 2·r )²
Oberfläche: A = 2·π·r·( h + r )
Mantelfläche: M = 2·π·r·h
Volumen: V = π·r²·h

Mit:
r: Radius der Kugel
h: Höhe der Kugelschicht
 
Kegel:

Mantellinie: m = √ h² + r²
Mantelfläche: M = r·m·π
Oberfläche: A = r·π·( r + m )
Volumen: V = 1/3·r²·π·h
Öffnungswinkel: α = 2·arcsin( r / m )

Mit:
h: Höhe des Kegels
r: Radius der Grundfläche des Kegels
 
Prisma:

Allgemeine Zusammenhänge:

Oberfläche: O = 2·A_G+M
Mantelfläche: M = U_G·h
Volumen: V = A_G·h

Mit rechtwinkligem Dreieck als Grundfläche:

Grundfläche: A_G = a·b/2
Umfang der Grundfläche: U_G = a+b+c
 
Mit gleichschenkligem Dreieck als Grundfläche:

Grundfläche: A_G = c·h_c/2 bzw. A_G = a·h_a/2
Umfang der Grundfläche: U_G = 2·a+c
 
Mit gleichseitigem Dreieck als Grundfläche:

Grundfläche: A_G = a²·√3/4
Umfang der Grundfläche: U_G = 2·a+c
 
Mit allgemeinem Dreieck als Grundfläche:

Grundfläche: A_G = a·ha/2  bzw. A_G = b·hb/2  bzw. A_G = c·hc/2
Umfang der Grundfläche: U_G = a+b+c

Mit:
a,b,c: Seiten der Grundfläche des Prismas
A_G: Grundfläche des Prismas
h: Höhe des Prismas
h_a,h_b,h_c: Höhen der Dreiecke der Grundfläche des Prismas

Quadratische Pyramide:
 
Grundfläche: A_g = a²
Höhe der Seitenfläche: h_a = √ h² + (a/2)²
Diagonale: d = √ 2·a
Seitenkante: s = √ h_a² + a²/2
Umfang: U = 4·a
Grundfläche: A_G = a²
Mantelfläche: M = 2·a·h_a
Oberfläche: O = A_G + M
Volumen: V = h·a²/3
Neigung der Seitenkante: α = arctan(h_a/2)
Neigung der Seitenfläche: β = arctan(h/(√ 2·a/2))
Seitenfläche: A_s = a/2·h_a

Mit:
a: Seitenlänge der Grundfläche
h: Höhe der Pyramide
 
Quadratischer Pyramidenstumpf:
 
Grundfläche: A_g = a²
Deckfläche: A_d = b²
Höhe der Seitenfläche: h_s = √ h² + ((a-b)/2)²
Seitenfläche: A_s = (a+b)/2·h_s
Mantelfläche: M = 4·A_s
Oberfläche: O = A_g+A_d+M
Volumen: V = (a²+a·b+b²)·h/3

Mit:
a: Seitenlänge der Grundfläche
b: Seitenlänge der Deckfläche
h: Höhe des Pyramidenstumpfs

Keil:

Schräge Kante: s = √ h² + [(a-c)/2]² + (b/2)²
Oberfläche: A = a·b + (a+c)·√ s² - [(a-c)/2]² + b·√ (4s² - b²) / 4
Volumen: V = b·h·(a/3 + c/6)

Mit:
a,b: Seitenlängen der Grundfläche
c: Länge der Scheitelkante
h: Höhe des Keils

Obelisk:
 
Höhe: h = k+m
Mantelfläche: M = ( a + b )·√ ( a - b )² + 4k² + b·√ 4m² + b²
Oberfläche: A = a² + M
Volumen: V = (k·(( a² + b² ) + √ ab ² ) + m·b²) / 3

Mit:
k: Höhe des Pyramidenstumpfs
m: Höhe der Pyramide
a: Länge der unteren Seite
b: Länge der Seite am Übergang
 
   
Im Folgenden sind einige in diesem Zusammenhang häufiger verwendete Fachworte kurz erklärt.

Körperberechnung: Das Wort Körperberechnung beschreibt in diesem Zusammenhang die für einen geometrischen Körper hinsichtlich seiner Eigenschaften durchzuführenden Berechnungen.

Volumenberechnung: Mit dem Begriff Volumenberechnung wird die Bestimmung des Volumens (Rauminhalts) geometrischer Körper angegeben.

Oberflächenberechnung: Mit dem Ausdruck Oberflächenberechnung wird die Berechnung der Oberfläche (Mantelfläche) geometrischer Körper bezeichnet.

Grundflächeninhalt: Das Wort Grundflächeninhalt bezeichnet den Flächeninhalt der Grundflächen eines geometrischen Körpers.

Teilflächen: Mit dem Begriff Teilfläche wird eine regelmäßige Fläche bezeichnet, die Teil einer allgemeinen Fläche (der Oberfläche eines Körpers) ist. Teilflächen setzen sich in diesem Zusammenhang aus bekannten regelmäßige Flächen wie Dreiecken, Rechtecken, Quadraten etc. zusammen.
 
Querschnittsfläche: Wird ein Körper senkrecht zu seiner Länge (quer) durchgeschnitten, so wird dieser Anschnitt die Querschnittsfläche des Körpers genannt.
 
Begrenzungsfläche: Die begrenzenden Flächen eines (geometrischen) Körpers werden Begrenzungsflächen genannt. Ihre Gesamtheit wird als Oberfläche des Körpers bezeichnet.

Seitenflächen: Als Seitenfläche wird ein abgegrenzter Teil der Oberfläche eines geometrischen Körpers bezeichnet.

Kantenlänge: Als Kantenlänge wird die Länge einer Seitenkante eines geradlinig begrenzten geometrischen Körpers bezeichnet.
Basiskante: Als Basiskante wird die Kante der Grundfläche eines geradlinig begrenzten geometrischen Körpers bezeichnet.

Mantellinie: Als Mantellinie wird bei einem geraden Kegel eine gerade Linie bezeichnet, die von der Spitze des Körpers zu einem Punkt des Grundkreises dessen verläuft. Bei einem Zylinder entspricht die Mantellinie dessen Höhe.
 
Körperhöhe: Die Körperhöhe ist der kürzeste Abstand (Normalabstand) der Grundfläche eines geometrischen Körpers bis zu dessen Spitze oder Deckfläche.
 
Volumenformel: Als Volumenformel wird die Formel bezeichnet, mit Hilfe derer das Volumen geometrischer Körper berechnet werden kann.
 
Kantenmodell: Unter einem Kantenmodell wird ein geometrischer Körper verstanden, der lediglich durch sein ihn begrenzenden Flächen dargestellt wird.
 
Schiefe Körper: Ein Körper heißt schief, wenn seine Grund- und Deckfläche kongruent zueinander sind, diese beiden Flächen parallel zueinander liegen und die Mantellinien dieser Körper nicht senkrecht auf der Grund- und Deckfläche stehen.

Stumpfe Körper: Als stumpfe Körper werden waagerecht abgeschnittene Pyramiden oder Kegel bezeichnet.

   
Als Schrägbilder werden Darstellungen von Körpern bezeichnet, die diesen auf einer ebenen Fläche dreidimendional erscheinen lassen. Abbildungen dieser Art werden auch Schrägriss genannt. Die Vorderseite (Vorderansicht) einer Zeichnung dieser Art bleibt unverändert und die Seitenflächen sowie die Deckfläche des Körpers werden in verkürzter Form dargestellt. Die Kanten des darzustellenden Körpers werden schräg nach hinten verlaufend gezeichnet. Alle zur Zeichenebene parallel verlaufenden Strecken, Flächen und Winkel besitzen wahre Größe und Strecken, die senkrecht zur Zeichenebene verlaufen, werden in verzerrter Form dargestellt.



Abb.1 - Schrägbild - Ohne verdeckte Kanten



Abb.2 - Schrägbild - Mit verdeckten Kanten

Der Winkel der diese Schräge beschreibt wird als Verzerrungswinkel α bezeichnet und mit meist 45° bemessen. Die schräg nach hinten verlaufenden Kanten des entsprechenden Körpers werden um den Verzerrungsfaktor 0,5 verkürzt dargestellt und parallel verlaufende Kanten behalten ihre Parallelität bei. Auch der Gebrauch eines Verzerrungswinkels von 30° und die Verwendung eines Verkürzungsfaktors von 1/3 oder eines Verzerrungswinkels von 60° und eines Verkürzungsfaktors von 2/3 sind gebräuchlich.
   
Nachfolgend ist die kurze Beschreibung einiger Arten häufig zu berechnender Pyramiden und Prismen zu finden.

1. Pyramiden:

Eine quadratische Pyramide stellt eine Pyramide dar, deren Grundfläche aus einem Quadrat besteht. Handelt es sich um eine gerade quadratische Pyramide, so bestehen ihre Mantelflächen aus vier gleichschenkligen konguenten Dreiecken. Ihre Spitze steht in diesem Fall senkrecht über der Mitte des Quadrats.

Eine dreiseitige Pyramide (dreieckige Pyramide oder Dreieckspyramide) besitzt ein Dreieck als Grundfläche. Die drei Eckpunkte dieser Grundfläche sind mit der Pyramidenspitze verbunden. Ihre Mantelfläche setzt sich aus drei gleichschenkligen Dreiecken zusammen.

Eine vierseitige Pyramide (viereckige Pyramide) besitzt ein Viereck als Grundfläche. Die vier Eckpunkte dieser Grundfläche sind mit der Pyramidenspitze verbunden. Sie besitzt drei dreieckige Seitenflächen. Ihre Mantelfläche setzt sich aus vier gleichschenkligen Dreiecken zusammen.

Eine fünfseitige Pyramide (fünfeckige Pyramide) besitzt ein Fünfeck als Grundfläche. Die fünf Eckpunkte dieser Grundfläche sind mit der Pyramidenspitze verbunden. Sie besitzt vier dreieckige Seitenflächen. Ihre Mantelfläche setzt sich aus fünf gleichschenkligen Dreiecken zusammen.

Eine sechsseitige Pyramide (sechseckige Pyramide) besitzt ein Sechseck als Grundfläche. Die sechs Eckpunkte dieser Grundfläche sind mit der Pyramidenspitze verbunden. Sie besitzt fünf dreieckige Seitenflächen. Ihre Mantelfläche setzt sich aus sechs gleichschenkligen Dreiecken zusammen.

Eine achtseitige Pyramide (achteckige Pyramide) besitzt ein Achteck als Grundfläche. Die acht Eckpunkte dieser Grundfläche sind mit der Pyramidenspitze verbunden. Sie besitzt sieben dreieckige Seitenflächen. Ihre Mantelfläche setzt sich aus acht gleichschenkligen Dreiecken zusammen.

Bei einer n-eckigen Doppelpyramide handelt es sich um einen Polyeder, der entsteht, wenn eine n-eckige Pyramide und ihr Spiegelbild an deren Grundflächen verbunden werden.

---

2. Prismen:

Ein dreiseitiges Prisma (Dreiecksprisma) besitzt eine dreieckige Grund- und Deckfläche. Diese Flächen können allgemeine, rechtwinkelige, gleichschenklige oder gleichseitige Dreiecke sein. Ein Prisma dieser Art besitzt 3 Seitenflächen, die Rechtecke sind und deren Höhen identisch sind. Es verfügt somit über 5 Begrenzungsflächen, 6 Eckpunkte sowie 9 Kanten. Als gerades dreiseitiges Prisma wird ein Prisma dieser Art bezeichnet, wenn es senkrecht auf dessen Grundfläche stehende Seitenflächen besitzt. Ein Prisma das eine trapezförmige Grundfläche besitzt, wird trapezförmiges Prisma genannt.
 
Ein vierseitiges Prisma besitzt eine viereckige Grund- und Deckfläche. Diese Flächen können Rechtecke oder Quadrate sein. Handelt es sich bei der Grund- und Deckfläche um ein jeweils gleich großes Quadrat, so wird dieser Körper als quadratisches Prisma bezeichnet. Ein vierseites Prisma besitzt 4 Seitenflächen, die Rechtecke sind und deren Höhen identisch sind. Es verfügt somit über 6 Begrenzungsflächen, 8 Eckpunkte sowie 12 Kanten. Ein rechteckiges Prisma ist ein vierseitiges Prisma, welches als Grund- und Deckfläche zwei kongruente Rechtecke besitzt.

Ein fünfseitiges Prisma besitzt eine fünfeckige Grund- und Deckfläche. Diese Flächen sind regelmäßige oder unregelmäßige Fünfecke. Ein Prisma dieser Art besitzt 5 Seitenflächen, die Rechtecke sind und deren Höhen identisch sind. Es verfügt somit über 7 Begrenzungsflächen, 10 Eckpunkte sowie 15 Kanten.

Ein sechsseitiges Prisma (Sechseckprisma oder sechseckiges Prisma) besitzt eine sechseckige Grund- und Deckfläche. Diese Flächen sind regelmäßige oder unregelmäßige Sechsecke. Ein Prisma dieser Art besitzt 6 Seitenflächen, die Rechtecke sind und deren Höhen identisch sind. Es verfügt somit über 8 Begrenzungsflächen, 12 Eckpunkte sowie 18 Kanten.

Ein achtseitiges Prisma besitzt eine achteckige Grund- und Deckfläche. Diese Flächen sind regelmäßige oder unregelmäßige Achtecke. Ein Prisma dieser Art besitzt 8 Seitenflächen, die Rechtecke sind und deren Höhen identisch sind. Es verfügt somit über 10 Begrenzungsflächen, 14 Eckpunkte sowie 21 Kanten.
 
   
Das Gewicht eines Körpers errechnet sich aus der Masse dessen sowie der Dichte des Materials aus welchem er besteht.

Seine Dichte kann wie folgt berechnet werden:

ρ = m/V

Sein Gewicht errechnet sich mit:

G = m · g

ρ: Dichte des Materials des Körpers [kg/dm³]
m: Masse des Körpers [kg]
V: Volumen des Körpers [dm³]
g: Erdbeschleunigung = 9,81 m/s²
  

 

Grafische Darstellung - Beispiel 1 - Doppelpyramide


Grafische Darstellung - Beispiel 2 - Kegel


Grafische Darstellung - Beispiel 3 - Keil


Grafische Darstellung - Beispiel 4 - Obelisk


Grafische Darstellung - Beispiel 5 - Regelmäßiges Prisma


Grafische Darstellung - Beispiel 6 - Schiefes Prisma


Grafische Darstellung - Beispiel 7 - Regelmäßige Pyramide


Grafische Darstellung - Beispiel 8 - Vierseitige Pyramide


Grafische Darstellung - Beispiel 9 - Pyramidenstumpf


Grafische Darstellung - Beispiel 10 - Schiefe Pyramide


Grafische Darstellung - Beispiel 11 - Zylinder

  

Körperberechnung und grafische Darstellung

 
Gehen Sie folgendermaßen vor, um Berechnungen mit Körpern der oben aufgeführten Arten durchzuführen und sich diese grafisch ausgeben zu lassen:
 

1. Wählen Sie, durch die Fokussierung des entsprechenden Eintrags in der Tabelle, den Körper mit dem Berechnungen durchgeführt werden sollen.
    
2. Geben Sie die erforderlichen Werte der Größen in die dafür vorgesehenen Felder ein. Bedienen Sie ggf. zuvor die Schaltfläche Löschen.
    
3. Führen Sie einen Klick auf die Schaltfläche Berechnen aus.
    
4. Bestimmen Sie mit Hilfe der aufklappbaren Auswahlbox Auswahl die Art, wie Sie Körper dargestellt bekommen möchten. Hierzu stehen die unten aufgeführten Möglichkeiten zur Verfügung.
    
5. Soll der Schwerpunkt des Körpers dargestellt werden, so aktivieren Sie das Kontrollkästchen Schwerpunkt. Um einen Körper ohne Grund- bzw. Deckfläche(n) darstellen zu lassen, aktivieren Sie das Kontrollkästchen Ohne Grund- und Deckfläche. Besitzen die Körper regelmäßige Polygone als Deck- bzw. Bodenfläche so können durch eine Aktivierung des Kontrollkästchens In- und Umkreis außerdem die entsprechenden In- bzw. Umkreise der Polygone dargestellt werden.
    
6. Bedienen Sie hierauf die Schaltfläche Darstellen um sich den Körper grafisch ausgeben zu lassen.
    
7. Auf dem Bedienformular wird bei Ausgabe der grafischen Darstellung die Möglichkeit geboten, einen dargestellten Körper plan bzgl. der x-z-Ebene (bis zu dessen Mitte) aufzuschneiden und somit sein "Inneres" zu untersuchen. Benutzen Sie hierfür den Rollbalken mit der Bezeichnung Schnitt bei y =.

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

   
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
 
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Berechnung

Nachfolgend aufgeführt finden Sie die zur Durchführung einer numerischen Berechnung benötigten Eingabewerte, sowie die vom Programm numerisch ermittelten Berechnungsergebnisse.
 
Erforderliche Eingaben:

 
Zur Berechnung eines regelmäßigen Prismas sind die Werte von genau 2 der 7 nachfolgend aufgeführten Größen einzugeben:

• Eckenanzahl n
• Länge der Seite s
• Höhe h
• Inkreisradius ri
• Umkreisradius ru
• Volumen (Rauminhalt) V
• Grundfläche Ag
• Oberfläche (Oberflächeninhalt) Ao

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Eckenanzahl n des Prismas
• Radius ru des Umkreises der Polygondeck- bzw. Polygonbodenfläche des Prismas
• Höhe h des Prismas
• Radius ri des Inkreises der Polygondeck- bzw. Polygonbodenfläche des Prismas
• Grundfläche Ag des Prismas (Boden- und Deckfläche)
• Mantelfläche (Mantelflächeninhalt) Am des Prismas
• Gesamtoberfläche (Oberflächeninhalt) Ao des Prismas
• Länge s der Seitenkante des Prismas
• Volumen (Rauminhalt) V des Prismas
• Koordinaten des Schwerpunkts S des Prismas

 

Erforderliche Eingaben:

Zur Berechnung eines senkrechten Zylinders sind die Werte von genau 2 der 7 nachfolgend aufgeführten Größen einzugeben:

• Radius r
• Höhe h
• Umfang U
• Volumen (Rauminhalt) V
• Mantelfläche (Mantelflächeninhalt) Am
• Grundfläche Ag
• Oberfläche (Oberflächeninhalt) Ao

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Umfang U des Zylinders
• Grundfläche Ag des Zylinders
• Mantelfläche (Mantelflächeninhalt) Am des Zylinders
• Gesamtoberfläche (Oberflächeninhalt) Ao des Zylinders
• Volumen (Rauminhalt) V des Zylinders
• Koordinaten des Schwerpunkts S des Zylinders

 

Erforderliche Eingaben:

Zur Berechnung einer vierseitigen Pyramide sind die Werte von genau 2 der 7 nachfolgend aufgeführten Größen einzugeben:

• Grundkante a
• Seitenkante s
• Höhe h1
• Höhe der Seitenfläche h2
• Volumen (Rauminhalt) V
• Gesamtoberfläche (Oberflächeninhalt) Ao der Pyramide
• Flächeninhalt As einer Seitenfläche

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Länge a der Grundkante der Pyramide
• Höhe h1 der Pyramide
• Umkreisradius ru der Bodenfläche der Pyramide
• Inkreisradius ri der Bodenfläche der Pyramide
• Länge s der Seitenkante der Pyramide
• Höhe h2 der Seitenfläche der Pyramide
• Kantenwinkel (in Grad) der Pyramide
• Seitenflächenwinkel (in Grad) der Pyramide
• Flächeninhalt As einer Seitenfläche der Pyramide
• Gesamtflächeninhalt Aa aller Seitenflächen der Pyramide
• Flächeninhalt Ab der Bodenfläche der Pyramide
• Gesamtoberfläche Ao der Pyramide
• Volumen (Rauminhalt) V der Pyramide
• Koordinaten des Schwerpunkts S der Pyramide

 

Erforderliche Eingaben:

Zur Berechnung eines senkrechten Kreiskegels sind die Werte von genau 2 der 7 nachfolgend aufgeführten Größen einzugeben:

• Radius r
• Höhe h
• Länge der Mantellinie s
• Volumen (Rauminhalt) V
• Mantelfläche (Mantelflächeninhalt) Am
• Grundfläche Ag
• Oberfläche (Oberflächeninhalt) Ao

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Mantelfläche (Mantelflächeninhalt) Am des Kegels
• Grundfläche Ag des Kegels
• Gesamtoberfläche (Oberflächeninhalt) Ao des Kegels
• Länge s der Seitenlinie des Kegels
• Umfang Uk des Grundkreises des Kegels
• Neigungswinkel der Seitenlinie des Kegels (in Grad)
• Volumen (Rauminhalt) V des Kegels
• Koordinaten des Schwerpunkts S des Kegels

 

Erforderliche Eingaben:

Zur Berechnung einer Kugel ist der Wert genau einer der 4 nachfolgend aufgeführten Größen einzugeben:

• Radius r
• Umfang U
• Oberfläche (Oberflächeninhalt) A
• Volumen (Rauminhalt) V

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Radius r der Kugel
• Umfang U der Kugel
• Oberfläche (Oberflächeninhalt) A der Kugel
• Volumen (Rauminhalt) V der Kugel
• Koordinaten des Schwerpunkts S der Kugel

 

Erforderliche Eingaben:

Zur Berechnung eines Keils sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Länge der Seite a
• Länge der Seite b
• Länge der Seite a1
• Höhe h

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Länge der Seite a des Keils
• Länge der Seite b des Keils
• Länge der Seite a1 des Keils
• Höhe h des Keils
• Flächeninhalt As aller Seitenflächen des Keils
• Flächeninhalt Ab der Bodenfläche des Keils
• Gesamtflächeninhalt Ag des Keils
• Volumen (Rauminhalt) V des Keils
• Koordinaten des Schwerpunkts S des Keils

 

Erforderliche Eingaben:

Zur Berechnung eines Obelisks sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Länge der Seite a
• Länge der Seite b
• Länge der Seite a1
• Länge der Seite b1
• Höhe h

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Länge der Seite a des Obelisks
• Länge der Seite b des Obelisks
• Länge der Seite a1 des Obelisks
• Länge der Seite b1 des Obelisks
• Höhe h des Obelisks
• Flächeninhalt As aller Seitenflächen des Obelisks
• Flächeninhalt Ab beider Grundflächen des Obelisks
• Gesamtflächeninhalt Ag des Obelisks
• Volumen (Rauminhalt) V des Obelisks
• Koordinaten des Schwerpunkts S des Obelisks

 

Erforderliche Eingaben:

Zur Berechnung einer Doppelpyramide sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Eckenanzahl n
• Umkreisradius ru1 des oben liegenden Polygons (Deckfläche)
• Höhe h1
• Umkreisradius ru2 des unten liegenden Polygons (Bodenfläche)
• Höhe h2

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

Für die oben angeordnete Pyramide:

• Umkreisradius ru der Pyramide
• Höhe h der Pyramide
• Inkreisradius ri der Pyramide
• Grundkantenlänge a der Pyramide
• Seitenkantenlänge s der Pyramide
• Flächeninhalt Aa aller Seitenflächen der Pyramide
• Flächeninhalt Ab der Bodenfläche der Pyramide
• Gesamtoberfläche Ao der Pyramide
• Kantenwinkel (in Grad) der Pyramide
• Seitenflächenwinkel (in Grad) der Pyramide
• Volumen (Rauminhalt) V der Pyramide

Für die unten angeordnete Pyramide:

• Umkreisradius ru der Pyramide
• Höhe h der Pyramide
• Inkreisradius ri der Pyramide
• Grundkantenlänge a der Pyramide
• Seitenkantenlänge s der Pyramide
• Flächeninhalt Aa aller Seitenflächen der Pyramide
• Flächeninhalt Ab der Bodenfläche der Pyramide
• Gesamtoberfläche Ao der Pyramide
• Kantenwinkel (in Grad) der Pyramide
• Seitenflächenwinkel (in Grad) der Pyramide
• Volumen (Rauminhalt) V der Pyramide

Für beide Pyramiden:

• Gesamtflächeninhalt Ag beider Pyramiden
• Gesamtvolumen Vg beider Pyramiden

 

Erforderliche Eingaben:

Zur Berechnung eines Pyramidenstumpfs sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Eckenanzahl n
• Umkreisradius ru1
• Umkreisradius ru2
• Höhe h

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Eckenanzahl n des Pyramidenstumpfs
• Höhe h des Pyramidenstumpfs
• Umkreisradius ru der Deckfläche des Pyramidenstumpfs
• Inkreisradius ri der Deckfläche des Pyramidenstumpfs
• Kantenlänge a der Grundkante der Deckfläche des Pyramidenstumpfs
• Flächeninhalt Ad der Deckfläche des Pyramidenstumpfs
• Umkreisradius ru der Bodenfläche des Pyramidenstumpfs
• Inkreisradius ri der Bodenfläche des Pyramidenstumpfs
• Kantenlänge a der Grundkante der Bodenfläche des Pyramidenstumpfs
• Flächeninhalt Ab der Bodenfläche des Pyramidenstumpfs
• Mantelfläche M des Pyramidenstumpfs
• Gesamtflächeninhalt Ao des Pyramidenstumpfs
• Länge s der Seitenkante des Pyramidenstumpfs
• Mittlerer Querschnitt Am des Pyramidenstumpfs
• Kantenwinkel (in Grad) des Pyramidenstumpfs
• Seitenflächenwinkel (in Grad) des Pyramidenstumpfs
• Volumen (Rauminhalt) V des Pyramidenstumpfs
• Koordinaten des Schwerpunkts S des Pyramidenstumpfs

 

Erforderliche Eingaben:

Zur Berechnung eines Pyramidenstumpfs sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Eckenanzahl n
• Umkreisradius ru
• Höhe h
• Koordinatenwerte des Mittelpunkts M (x / y) des oberen Umkreises des Prismas

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Eckenanzahl n des Prismas
• Höhe h des Prismas
• Radius ru des Umkreises des Prismas
• Koordinatenwerte des Mittelpunkts M (x / y) der Unterseite des Prismas
• Radius ri des Inkreises der Polygondeck- bzw. Polygonbodenfläche des Prismas
• Grundfläche Ag des Prismas (Boden- und Deckfläche)
• Mantelfläche Am des Prismas
• Gesamtoberfläche (Oberflächeninhalt) Ao des Prismas
• Länge s der Seitenkante des Prismas
• Volumen (Rauminhalt) V des Prismas
• Koordinaten des Schwerpunkts S des Prismas

 

Erforderliche Eingaben:

Zur Berechnung einer schiefen Pyramide sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

• Eckenanzahl n
• Umkreisradius ru
• Höhe h
• Koordinatenwerte der Spitze M (x / y) der Pyramide

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Eckenanzahl n der Pyramide
• Umkreisradius ru der Pyramide
• Höhe h der Pyramide
• Koordinatenwerte der Spitze M (x / y) der Pyramide
• Länge a der Grundkante der Pyramide
• Radius ri des Inkreises der Bodenfläche der Pyramide
• Flächeninhalt Aa aller Seitenflächen der Pyramide
• Flächeninhalt Ab der Bodenfläche der Pyramide
• Flächeninhalt Ao der Gesamtoberfläche der Pyramide
• Volumen (Rauminhalt) V der Pyramide
• Koordinaten des Schwerpunkts S der Pyramide

 

Erforderliche Eingaben:

Zur Berechnung einer n-seitigen Pyramide sind alle Werte der nachfolgend aufgeführten Größen einzugeben:

Wird der Kontrollschalter Umkreisradius aktiviert, so sind dies:

• Eckenanzahl n
• Umkreisradius ru
• Höhe h

Wird der Kontrollschalter Grundkantenlänge aktiviert, so sind dies:

• Eckenanzahl n
• Grundkantenlänge a
• Höhe h

Ermittelte Ergebnisse:

Sind mit den Eingaben Berechnungen durchführbar, so gibt das Programm aus:

• Eckenanzahl n der Pyramide
• Umkreisradius ru der Pyramide
• Höhe h der Pyramide
• Radius ri des Inkreises der Bodenfläche der Pyramide
• Länge a der Grundkante der Pyramide
• Länge s der Seitenkante der Pyramide
• Kantenwinkel (in Grad) der Pyramide
• Seitenflächenwinkel (in Grad) der Pyramide
• Flächeninhalt As einer Seitenfläche der Pyramide
• Flächeninhalt Aa aller Seitenflächen der Pyramide
• Flächeninhalt Ab der Bodenfläche der Pyramide
• Flächeninhalt Ao der Gesamtoberfläche der Pyramide
• Volumen (Rauminhalt) V der Pyramide
• Koordinaten des Schwerpunkts S der Pyramide 

 

 

Bei der Darstellung von Gebilden ermöglicht das Programm die Bemessung des Darstellungsbereichs auf eine der folgenden Arten und Weisen:
 

• Automatisch

• Statisch

1. Automatisch:

   Wird die Einstellung Automatisch durch die Aktivierung des entsprechenden Kontrollschalters gewählt, so ermittelt das Programm alle zur vollständigen Darstellung des Körpers erforderlichen x-, y- und z-Koordinatenwerte automatisch und bemisst den Darstellungsbereich dementsprechend.
    

2. Statisch:
   Wird der Kontrollschalter Statisch aktiviert, so verwendet das Programm bei Aufruf der Darstellung den unter Abs. Bereich voreingestellten Darstellungsbereich und beschneidet den Körper an Stellen, die außerhalb dessen liegen. Diesen Bereich können Sie bei Ausgabe der Darstellung verändern, indem Sie den auf dem Bedienformular zur Verfügung stehenden Rollbalken Zoom positionieren. Der maximal einstellbare Wert entspricht dem Doppelten des, unter Abs. Bereich auf dem Hauptformular des Unterprogramms, vorgegebenen Werts.

 

 

Durch die Bedienung der aufklappbaren Auswahlbox im Formularbereich Darstellung - Optionen werden zudem folgende Optionen zur Verfügung gestellt, das Layout eines dargestellten Körpers zu beeinflussen:
 

• Gefüllt - Kanten als Rohre: Darstellung der Körperkanten als Rohre

• Gefüllt - Ohne Kantenmarkierung: Darstellung der Körperkanten ohne Begrenzungsmarkierung

 

 

Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.

 

 

Krummflächig begrenzte Körper
 

 

Beispiel 1 - Regelmäßiges Prisma:

 

Gegeben sei ein regelmäßiges Prisma, von dem die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 5
Länge der Seite: s = 5
Höhe: h = 4
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

Nach Auswahl des Tabelleneintrags Regelmäßiges Prisma, der Eingabe der Werte für die Eckenanzahl n, die Länge s der Seite sowie die Höhe h des Prismas und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

Radius des Umkreises der Polygondeck- bzw. Polygonbodenfläche ru:4 ,253
Höhe des Prismas h: 4
Radius des Inkreises der Polygondeck- bzw. Polygonbodenfläche ri: 3,441
Grundfläche des Prismas (Boden- und Deckfläche) Ag: 43,012 FE
Mantelfläche des Prismas Am: 100 FE
Gesamtoberfläche des Prismas Ao: 186,024 FE
Länge der Seitenkante s: 5
Volumen des Prismas V: 172,048 VE
Koordinaten des Schwerpunkts des Prismas: S (0 / 0 / 0)

 

Beispiel 2 - Senkrechter Zylinder:

Gegeben sei ein senkrechter Zylinder, von dem die Werte folgender Größen bekannt sind:

Radius: r = 3
Höhe: h = 1
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Senkrechter Zylinder, der Eingabe der Werte für den Radius r sowie für die Höhe h des Zylinders und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

 

 der Eingabe der Werte für den Radius rund die Höhe h des Zylinders

 

Umfang des Zylinders U: 18,85
Grundfläche des Zylinders Ag: 28,274 FE
Mantelfläche des Zylinders Am: 18,85 FE
Gesamtoberfläche des Zylinders Ao: 75,398 FE
Volumen des Zylinders V: 28,274 VE
Koordinaten des Schwerpunkts des Zylinders: S (0 / 0 / 0)

 

Beispiel 3 - Vierseitige Pyramide:

 

Gegeben sei eine vierseitige Pyramide, von der die Werte folgender Größen bekannt sind:

Grundkante: a = 4
Höhe: h1 = 3
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Vierseitige Pyramide, der Eingabe der Werte für die Grundkante a sowie für die Höhe h1 der Pyramide und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

 

Umkreisradius der Bodenfläche ru: 2,828
Inkreisradius der Bodenfläche ri: 2
Länge der Seitenkante s: 4,123
Höhe der Seitenfläche h2: 3,606
Kantenwinkel: 46,686°
Seitenflächenwinkel: 56,31°
Flächeninhalt einer Seitenfläche As: 7,211 FE
Gesamtflächeninhalt aller Seitenflächen Aa: 28,844 FE
Flächeninhalt der Bodenfläche Ab: 16 FE
Gesamtoberfläche der Pyramide Ao: 44,844 FE
Volumen der Pyramide V: 16 VE
Koordinaten des Schwerpunkts der Pyramide: S (0 / 0 / 0,75)

 

Beispiel 4 - Senkrechter Kreiskegel:

Gegeben sei ein senkrechter Kreiskegel, von dem die Werte folgender Größen bekannt sind:

Radius: r = 5
Höhe: h = 8
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Senkrechter Kreiskegel, der Eingabe der Werte für den Radius r sowie für die Höhe h des Kreiskegels und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

 

Mantelfläche des Kegels Am: 148,189 FE
Grundfläche des Kegels Ag: 78,54 FE
Gesamtoberfläche des Kegels Ao: 226,728 FE
Länge der Seitenlinie s: 9,434
Umfang des Grundkreises Uk: 31,416
Neigungswinkel der Seitenlinie des Kegels: 57,995°
Volumen des Kegels V: 209,44 VE
Koordinaten des Schwerpunkts des Kegels: S (0 / 0 / 2)

 

Beispiel 5 - Kugel:

 

Gegeben sei eine Kugel, von welcher der Wert folgender Größe bekannt ist:

Radius: r = 3
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Kugel, der Eingabe des Werts für den Radius der Kugel und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

Umfang U: 18,85
Oberfläche A: 113,097 FE
Volumen V: 113,097 VE
Koordinaten des Schwerpunkts: S (0 / 0 / 0)

 

Beispiel 6 - Keil:

 

Gegeben sei ein Keil, von dem die Werte folgender Größen bekannt sind:

Länge der Seite a: 5
Länge der Seite b: 2
Länge der Seite a1: 4
Höhe: h = 3

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Keil, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

Flächeninhalt aller Seitenflächen As: 24,815 FE
Flächeninhalt der Bodenfläche Ab: 10 FE
Gesamtflächeninhalt des Keils Ag: 34,815 FE
Volumen des Keils V: 14 VE
Koordinaten des Schwerpunkts des Keils: S (0 / 0 / 0,964)

 

Beispiel 7 - Obelisk:

Gegeben sei ein Obelisk, von dem die Werte folgender Größen bekannt sind:

Länge der Seite a: 8
Länge der Seite b: 7
Länge der Seite a1: 4
Länge der Seite b1: 2
Höhe: h = 5

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Obelisk, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

 

Flächeninhalt aller Seitenflächen As: 115,49 FE
Flächeninhalt beider Grundflächen Ab: 64 FE
Gesamtflächeninhalt des Obelisks Ag: 179,549 FE
Volumen des Obelisks V: 153,333 VE
Koordinaten des Schwerpunkts des Obelisks: S (0 / 0 / 1,082)

 

Beispiel 8 - Doppelpyramide:

 

Gegeben sei eine Doppelpyramide, von der die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 7
Umkreisradius des oben liegenden Polygons (Deckfläche): ru1 = 2
Höhe h1: 3
Umkreisradius des unten liegenden Polygons (Bodenfläche): ru2 = 3
Höhe h2: 4

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Doppelpyramide, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

Für die oben angeordnete Pyramide:
 

Inkreisradius ri: 1,802
Grundkantenlänge a: 1,736
Seitenkantenlänge s: 3,606
Flächeninhalt aller Seitenflächen Aa: 21,258 FE
Flächeninhalt der Bodenfläche Ab: 10,946 FE
Gesamtoberfläche der Pyramide Ao: 32,203 FE
Kantenwinkel: 63,435°
Seitenflächenwinkel: 65,749°
Volumen der Pyramide V: 10,946 VE

Für die unten angeordnete Pyramide:
 

Inkreisradius ri: 2,703
Grundkantenlänge a: 2,603
Seitenkantenlänge s: 5
Flächeninhalt aller Seitenflächen Aa: 43,987 FE
Flächeninhalt der Bodenfläche Ab: 24,628 FE
Gesamtoberfläche der Pyramide Ao: 68,615 FE
Kantenwinkel: 53,13°
Seitenflächenwinkel: 55,952°
Volumen der Pyramide: 32,837 VE

 

Für beide Pyramiden:

Gesamtflächeninhalt beider Pyramiden Ag: 100,818 FE
Gesamtvolumen beider Pyramiden Vg: 43,783 VE

 

Beispiel 9 - Pyramidenstumpf:

Gegeben sei ein Pyramidenstumpf, von dem die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 6
Umkreisradius ru1: 2
Umkreisradius ru2: 4
Höhe: h = 3

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Pyramidenstumpf, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

Umkreisradius der Deckfläche ru: 2
Inkreisradius der Deckfläche ri: 1,732
Kantenlänge der Grundkante der Deckfläche a: 2
Flächeninhalt der Deckfläche Ad: 10,392 FE
Umkreisradius der Bodenfläche ru: 4
Inkreisradius der Bodenfläche ri: 3,464
Kantenlänge der Grundkante der Bodenfläche a: 4
Flächeninhalt der Bodenfläche Ab: 41,569 FE
Mantelfläche des Pyramidenstumpfs M: 62,354 FE
Gesamtflächeninhalt des Pyramidenstumpfs Ao: 114,315 FE
Länge der Seitenkante s: 3,606
Mittlerer Querschnitt Am: 23,383 FE
Kantenwinkel: 56,31°
Seitenflächenwinkel: 60°
Volumen des Pyramidenstumpfs V: 72,746 VE
Koordinaten des Schwerpunkts des Pyramidenstumpfs: S (0 / 0 / -0,321)

 

Beispiel 10 - Schiefes Prisma:

Gegeben sei ein schiefes Prisma, von dem die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 5
Umkreisradius: ru = 3
Höhe: h = 6
Koordinatenwerte des Mittelpunkts M des oberen Umkreises des Prismas: M (3 / 1)

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Schiefes Prisma, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

Radius des Inkreises der Polygondeck- bzw. Polygonbodenfläche ri: 2,427
Grundfläche des Prismas (Boden- und Deckfläche) Ag: 21,399 FE
Mantelfläche des Prismas Am: 115,115 FE
Gesamtoberfläche des Prismas Ao: 157,913 FE
Länge der Seitenkante s: 3,527
Volumen des Prismas V: 128,393 VE
Koordinaten des Schwerpunkts des Prismas: S (1,5 / 0,5 / 0)

 

Beispiel 11 - Schiefe Pyramide:

Gegeben sei eine schiefe Pyramide, von der die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 10
Umkreisradius: ru = 3
Höhe: h = 3
Koordinatenwerte der Spitze der Pyramide: M (-1 / 3)

 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags Schiefe Pyramide, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

Länge der Grundkante a: 1,854
Radius des Inkreises der Bodenfläche ri: 2,853
Flächeninhalt aller Seitenflächen der Pyramide Aa: 41,67 FE
Flächeninhalt der Bodenfläche der Pyramide Ab: 26,45 FE
Flächeninhalt der Gesamtoberfläche der Pyramide Ao: 68,12 FE
Volumen der Pyramide V: 26,45 VE
Koordinaten des Schwerpunkts der Pyramide: S (-0,25 / 0,75 / 0,75)

 

Beispiel 12 - N-seitige Pyramide:

Gegeben sei eine n-seitige Pyramide, von der die Werte folgender Größen bekannt sind:

Eckenanzahl: n = 9
Umkreisradius: ru = 3
Höhe: h = 3
 

Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.

 

Vorgehensweise und Lösung:

 

Nach Auswahl des Tabelleneintrags N-seitige Pyramide, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

Radius des Inkreises der Bodenfläche ri: 2,819
Länge der Grundkante a: 2,052
Länge der Seitenkante s: 4,243
Kantenwinkel: 45°
Seitenflächenwinkel: 46,781°
Flächeninhalt einer Seitenfläche der Pyramide As: 4,224 FE
Flächeninhalt aller Seitenflächen der Pyramide Aa: 38,016 FE
Flächeninhalt der Bodenfläche der Pyramide Ab: 26,033 FE
Flächeninhalt der Gesamtoberfläche der Pyramide Ao: 64,049 FE
Volumen der Pyramide V: 26,033 VE
Koordinaten des Schwerpunkts der Pyramide: S (0 / 0 / 0,75)
 

 

Grafische Darstellung - Beispiel 12 - Regelmäßiges Prisma


Grafische Darstellung - Beispiel 13 - Prisma geschnitten


Grafische Darstellung - Beispiel 14 - Schiefes Prisma


Grafische Darstellung - Beispiel 15 - Schiefes Prisma


Grafische Darstellung - Beispiel 16 - Zylinder


Grafische Darstellung - Beispiel 17 - Zylinder geschnitten


Grafische Darstellung - Beispiel 18 - Kegel


Grafische Darstellung - Beispiel 19 - Kreiskegel geschnitten


Grafische Darstellung - Beispiel 20 - Keil


Grafische Darstellung - Beispiel 21 - Keil


Grafische Darstellung - Beispiel 22 - Obelisk


Grafische Darstellung - Beispiel 23 - Obelisk


Grafische Darstellung - Beispiel 24 - Vierseitige Pyramide


Grafische Darstellung - Beispiel 25 - Vierseitige Pyramide


Grafische Darstellung - Beispiel 26 - Doppelpyramide


Grafische Darstellung - Beispiel 27 - Doppelpyramide


Grafische Darstellung - Beispiel 28 - Pyramidenstumpf


Grafische Darstellung - Beispiel 29 - Pyramidenstumpf


Grafische Darstellung - Beispiel 30 - Schiefe Pyramide


Grafische Darstellung - Beispiel 31 - Schiefe Pyramide


Grafische Darstellung - Beispiel 32 - Pyramide


Grafische Darstellung - Beispiel 33 - Pyramide


Grafische Darstellung - Beispiel 34 - Kugel


Grafische Darstellung - Beispiel 35 - Kugel geschnitten

        
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Prisma
Wikipedia - Zylinder
Wikipedia - Pyramide
Wikipedia - Kegel
Wikipedia - Kugel
 
Hinweise und Bilder zu Abwicklungen einiger Körper dieser Art sind unter anderem auf der Seite Pyramidenstumpf zu erhalten.
 

 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
 

 

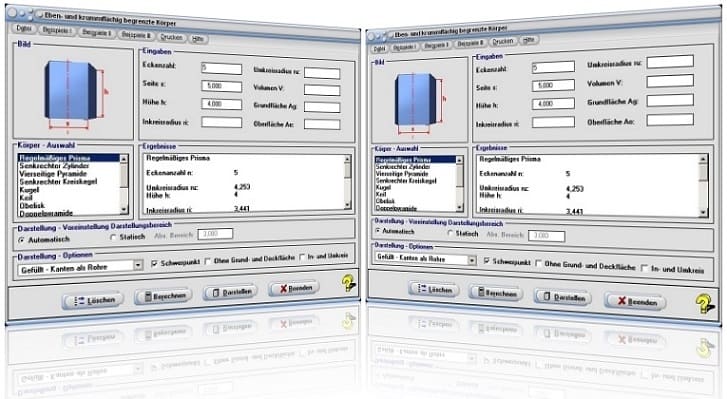
Startfenster des Unterprogramms Eben- und krummflächig begrenzte Körper
 

MathProf 5.0 - Startfenster des Unterprogramms Dreieck - Pyramide - Quader im Raum

---

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---