MathProf - Differentialgleichung höherer Ordnung - DGL - Lösen

 

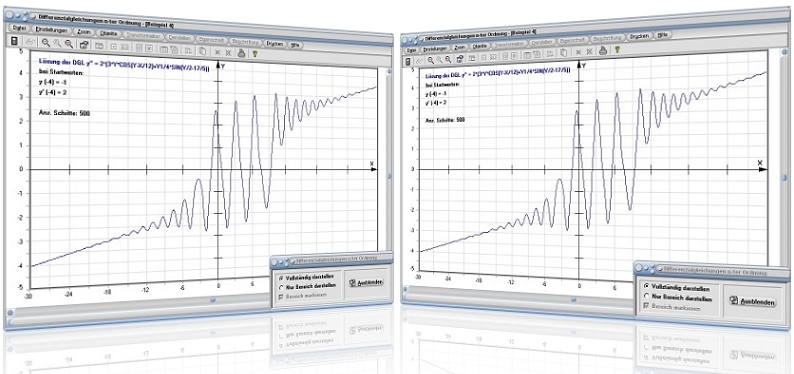
Modul DGL n-ter Ordnung

---

 
Das Unterprogramm [Algebra] - [Differentialgleichungen] - DGL n-ter (höherer) Ordnung ermöglicht es, Differentialgleichungen 2. Ordnung bis 8. Ordnung numerisch iterativ lösen zu lassen.

 

Eine Gleichung in der die n-te Ableitung einer unbekannten Funktion y = y(x) auftritt, wird als Differentialgleichung n-ter Ordnung bezeichnet. Eine Differentialgleichung kann als Bestimmungsgleichung für eine unbekannte Funktion aufgefasst werden. Dieses Unterprogramm ermittelt die Lösungskurve y = y(x) derartiger höherer Differentialgleichungen der:

 

DGL 2. Ordnung: y^'' = f(x,y,y')

DGL 3. Ordnung: y⁽³⁾ = f(x,y,y',y'')

DGL 4. Ordnung: y⁽⁴⁾ = f(x,y,y',y'',y⁽³⁾)

DGL 5. Ordnung: y⁽⁵⁾ = f(x,y,y',y'',y⁽³⁾,y⁽⁴⁾)

DGL 6. Ordnung: y⁽⁶⁾ = f(x,y,y',y'',y⁽³⁾,y⁽⁴⁾,y⁽⁵⁾)

DGL 7. Ordnung: y⁽⁷⁾ = f(x,y,y',y'',y⁽³⁾,y⁽⁴⁾,y⁽⁵⁾,y⁽⁶⁾)

DGL 8. Ordnung: y⁽⁸⁾ = f(x,y,y',y'',y⁽³⁾,y⁽⁴⁾,y⁽⁵⁾,y⁽⁶⁾,y⁽⁷⁾)
 
Treten in einer Gleichung neben der unabhängigen Variablen x und der von x abhängigen Variable y zudem noch Ableitungen der Funktion y auf, so wird von einer gewöhlichen Differentialgleichung gesprochen. Lösungsfunktionen von Differentialgleichungen werden als Lösung oder Integral bezeichnet.

Die Lösung einer Differentialgleichung n-ter Ordnung besitzt aufgrund der n-maligen mit ihr durchführbaren Integration n frei festlegbare Konstanten c_n. Sie stellt eine Kurvenschar mit n Parametern der Form F(x,y,c₁,c₂,c₃ ... c_n) dar.

Die Ordnung einer Differentialgleichung orientiert sich an der höchsten darin auftretenden Ableitung. Eine DGL wird als Differentialgleichung n-ter Ordnung bezeichnet, wenn die höchste darin vorkommende Ableitung die n-te Ableitung ist. Ein partikuläres Integral, bzw eine spezielle Lösung einer DGL ist jede Lösung, welche dadurch entsteht, dass einer Konstanten der allgemeinen Lösung ein bestimmter Wert zugeordnet wird.

Besteht die Möglichkeit, die allgemeine Lösung einer Differentialgleichung durch die Bildung von Kombinationen mit elementaren Funktionen zu ermitteln, so wird diese DGL als elementar integrierbar bezeichnet. Dies ist jedoch nur bei einigen bestimmten Typen von Gleichungen dieser Art möglich. Mit aus diesem Grund werden numerische Verfahren zur Ermittlung der Lösungen von DGL eingesetzt.
  

 

Wenden Sie die nachfolgend geschilderte Vorgehensweise an, um in diesem Modul Lösungskurven von DGL n-ter Ordnung ermitteln und grafisch ausgeben zu lassen:
 

1. Legen Sie die Ordnung der Differentialgleichung durch eine Bedienung des Steuerelements Ordnung der DGL fest.
    
2. Definieren Sie die zu analysierende Differentialgleichung, gemäß den geltenden Syntaxregeln, im dafür vorgesehenen Eingabefeld.
    
3. Tragen Sie in die Felder x0 =, y(x0) =, y'(x0) =, y''(x0) =  etc. die entsprechenden Startwerte (Anfangswerte) ein und legen Sie im Eingabefeld Bereich von x0 bis x1 = einen Maximalwert für x1 fest, über welchen die Ergebnisse ausgegeben werden sollen.
    
4. Legen Sie mittels dem zur Verfügung stehenden Rollbalken Anz. Schritte die Anzahl der bei Berechnungen durchzuführenden Schritte fest.
    
5. Bedienen Sie die Schaltfläche Berechnen.
    
6. Möchten Sie sich die Lösungskurve grafisch darstellen lassen, so bedienen Sie hierauf die Schaltfläche Darstellen.
    
7. Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters mit der Bezeichnung Nur Bereich darstellen bzw. Vollständig darstellen, ob die Lösungskurve über den gesamten Darstellungsbereich ausgegeben werden soll, oder lediglich innerhalb des festgelegten Intervallbereichs x0 < x < x1.
   
   Wurde der Kontrollschalter mit der Bezeichnung Nur Bereich darstellen gewählt, so legen Sie durch die Aktivierung des Kontrollkästchens Bereich markieren fest, ob bei der Darstellung der Lösungskurve eine Markierung des gewählten Intervallbereichs erfolgen soll.

Beachten Sie:

Für die Bezeichnungen der Ableitungen müssen Sie bei der Formulierung des Funktionsterms einer Differentialgleichung in diesem Unterprogramm folgende Zeichen verwenden:

 

1. Ableitung y': Y1

2. Ableitung y'': Y2

3. Ableitung y⁽³⁾: Y3

4. Ableitung y⁽⁴⁾: Y4

5. Ableitung y⁽⁵⁾: Y5

6. Ableitung y⁽⁶⁾: Y6

7. Ableitung y⁽⁷⁾: Y7

 

Hinweis:

Die Auflösungsgenauigkeit bei Ausgabe der grafischen Darstellung hängt von der gewählten Schrittanzahl zur numerischen Ermittlung der Lösungen ab. Je höher diese gewählt wird, desto exakter wird der Funktionsverlauf dargestellt.
 

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

DGL 1. Ordnung

DGL – Gleichungssystem

 

 

Wird die Differentialgleichung 2. Ordnung y'' = y'+2·y analytisch gelöst, so lautet die exakte Lösungsfunktion y = e^2·x + 2·e^-x.

 

Vorgehensweise:

 

Um die Lösungen dieser DGL im Intervall 0 < x < 1 numerisch ermitteln zu lassen, stellen Sie mit Hilfe des Steuerelements Ordnung der DGL den Wert 2 ein. Definieren Sie die Differentialgleichung y'' = y'+2·y, indem Sie in das Feld y'' = die Zeichenfolge Y1+2*Y (für die 1. Ableitung y' ist die Zeichenkombination Y1 zu verwenden) eingeben.

Legen Sie die Startwerte (Anfangswerte) x0 = 0, y(x0) = 3 und y'(x0) = 0 in den entsprechenden Eingabefeldern fest und geben Sie in das Feld Bereich von x0 bis x1 = den Wert 1 ein.

Positionieren Sie den Rollbalken Anz. Schritte auf 500, so erhalten Sie nach einer Bedienung der Schaltfläche Berechnen für die gestellten Anfangswertbedingungen folgende Ergebnisse (Auszug).
 

X	Y	Y'
0	3,00000	0
0,1	3,03108	0,63313
0,2	3,12929	1,34619
0,3	3,30376	2,16260
0,4	3,56618	3,11044
0,5	3,93134	4,22350
0,6	4,41774	5,54261
0,7	5,04837	7,11723
0,8	5,85169	9,00741
0,9	6,86279	11,28616
1,0	8,12481	14,04235

Wie zu erkennen ist, entsprechen diese numerisch ermittelten Werte denen, welche die analytisch ermittelte Funktion y = e^2·x + 2·e^-x in diesem Bereich besitzt, sehr gut.
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3

   

Grafische Darstellung - Beispiel 4
 

Grafische Darstellung - Beispiel 5
 

Grafische Darstellung - Beispiel 6

 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Differentialgleichung zu finden.

  

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
 

 

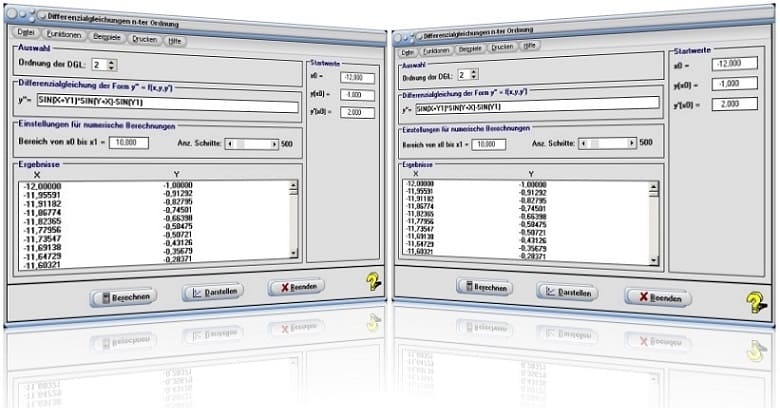
Startfenster des Unterprogramms Differentialgleichungen höherer Ordnung
 

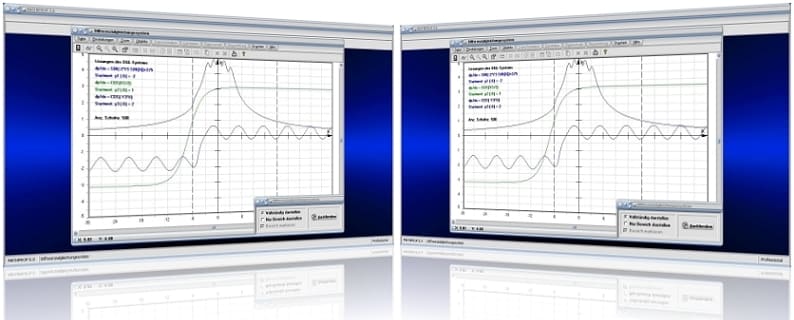
MathProf 5.0 - Unterprogramm Differentialgleichungssysteme 1. Ordnung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---