MathProf - Differentialgleichung 1. Ordnung - Differenzengleichung

   

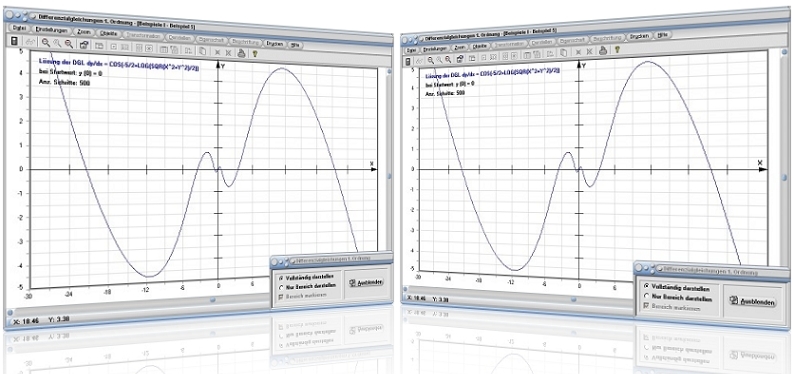
Modul DGL 1. Ordnung

---

Das Unterprogramm [Algebra] - [Differentialgleichungen] - DGL 1. Ordnung ermöglicht es, (u.a. lineare) Differentialgleichungen erster Ordnung numerisch iterativ lösen zu lassen.

 

 
Eine Gleichung in der die 1. Ableitung einer unbekannten Funktion y = y(x) auftritt, wird als Differentialgleichung 1. Ordnung bezeichnet. Eine Differentialgleichung (DGL) kann als Bestimmungsgleichung für eine unbekannte Funktion aufgefasst werden.

Die Ordnung einer Differentialgleichung orientiert sich an der höchsten darin auftretenden Ableitung. Eine DGL wird als Differentialgleichung erster Ordnung bezeichnet, wenn die höchste darin vorkommende Ableitung die erste Ableitung ist.
 
Treten in einer Gleichung dieser Art neben der unabhängigen Variablen x und der von x abhängigen Variable y zudem noch Ableitungen der Funktion y auf, so wird von einer gewöhnlichen Differentialgleichung gesprochen. Deren Bezeichnung lautet auch gewöhnliche DGL oder gewöhnliche DGL 1. Ordnung.

Lösungsfunktionen von Differentialgleichungen werden Lösung oder Integral genannt. Die Lösung einer Differentialgleichung erster Ordnung besitzt aufgrund der einmaligen mit ihr durchführbaren Integration eine frei festlegbare Konstante c. Sie stellt eine Kurvenschar mit einem Parameter der Form F(x,y,c) dar.
 
Ein partikuläres Integral, bzw. eine spezielle Lösung einer DGL ist jede Lösung, welche dadurch entsteht, dass der Konstanten der allgemeinen Lösung ein bestimmter Wert zugeordnet wird.
 
Eine lineare Differentialgleichung (lineare DGL) kann in folgender Form dargestellt werden:

yⁿ = f(x,y,y',y'', ... ,y^n-1)

Ist eine derartige Gleichung nicht in dieser Form darstellbar und kommt die Variable y, oder eine derer Ableitungen in einer nichtlinearen Funktion vor, so wird sie als nichtlineare Differentialgleichung (nichtlineare DGL) bezeichnet.

Die allgemeine Form einer Differentialgleichung besitzt die Gestalt:

f(y,y',y'', ... ,y^m) = b(x)

Der rechtsseitige Term b(x) einer derartigen DGL wird als Inhomogenität bezeichnet, oder mit dem Begriff Störfunktion beschrieben.

Besitzt der Term b(x) den Wert Null ( b(x) = 0 ), so trägt eine DGL dieser Art die Bezeichnung homogene Differentialgleichung (homogene DGL). Ist dieser hingegen nicht gleich Null ( b(x) ≠ 0 ), so wird sie inhomogene Differentialgleichung (inhomogene DGL) genannt.

Eine lineare Differentialgleichung erster Ordnung hat die Form:

y'′+g(x)y = h(x)

Ist die rechte Seite einer Gleichung dieser Art gleich 0, so handelt es sich um eine lineare homogene Differentialgleichung erster Ordnung. Sie besitzt die Form:

y′+g(x)y = 0


Exakte DGL (exakte Differentialgleichung): Eine Differentialgleichung heißt exakt oder total, wenn für sie eine Stammfunktion existiert.

---

Besteht die Möglichkeit, die allgemeine Lösung einer Differentialgleichung durch die Bildung von Kombinationen mit elementaren Funktionen zu ermitteln, so wird diese DGL als elementar integrierbar bezeichnet. Dies ist jedoch nur bei einigen bestimmten Typen von Gleichungen dieser Art möglich. Mit aus diesem Grund werden numerische Verfahren (numerische Methoden) zur Ermittlung der näherungsweisen Lösungen von DGL 1. Ordnung eingesetzt. Ein derartiges Verfahren wird als sukzessive Approximation oder schrittweise Annäherung bezeichnet.
 
Hierzu zählen das Runge-Kutta-Verfahren, die Heun-Methode (Heun-Verfahren) sowie die Euler-Methode (Euler-Verfahren). Die Nutzung dieser numerischen Lösungsverfahren für Differentialgleichungen (DGL) wird in diesem Modul ermöglicht.

Von einem Anfangswertproblem wird gesprochen, wenn die Lösung einer DGL 1. Ordnung durch einen definierten Punkt P(x₀,y₀) zu verlaufen hat. Als Randwertproblem wird eine Problemstellung bezeichnet, bei der es gilt, zu einer Differentialgleichung Lösungen zu suchen.
 
Ein Randwert gibt die an verschiedenen Stellen zu erfüllenden Bedingungen vor. Randwerte entscheiden über die Existenz sowie die Eindeutigkeit einer Lösung. Bei einem Randwertproblem sind die an den Rändern herrschenden Zustände bekannt. Bei einem Anfangswertproblem hingegen sind die Funktionswerte beim Anfangszeitpunkt bekannt.
 
Das explizite Euler-Verfahren (Eulersches Polygonzugverfahren) findet bei der numerischen Lösung eines Anfangswertproblems Einsatz. Es ist das einfachste Verfahren seiner Art und wurde von Leonhard Euler im Jahre 1768 in einem Buch vorgestellt und wird auch als Einschrittverfahren bezeichnet. Es wurde hierauf von Cauchy verwendet, um einige Beweise bzgl. der Eindeutigkeit gewöhnlicher Differentialgleichungen zu erbringen. Dieses Verfahren wird auch die Methode der kleinen Schritte genannt.

Bei dem sogenannten Heun-Verfahren, welches nach dem Mathematiker Karl Heun benannt ist, handelt es sich ebenfalls um ein Verfahren zur numerischen Bestimmung der Lösungen von Anfangswertaufgaben. Entgegen dem Euler-Verfahren findet hierbei die Näherung über ein Trapez und nicht über ein Rechteck statt.

Das Runge-Kutta-Verfahren (4.Ordnung) besitzt eine hohe Genauigkeit und findet daher mehr Einsatz als die zuvor beschriebenen Methoden. Auch bei diesem Verfahren wird die Lösungskurve der DGL 1. Ordnung mit dem festgelegten Anfangswert in jedem Teilintervall durch eine Gerade ersetzt. Im Gegensatz zum Euler-Verfahren (Streckenzugverfahren) wird hierbei für die Steigung der Geraden eine Art Mittelwert für die Steigung der Lösungskurve verwendet. Dieses Verfahren wird auch mit dem Kürzel RK4 bezeichnet oder als Mehrschrittverfahren bezeichnet.

Bei einer Differenzengleichung handelt es sich um eine Gleichung, die eine Differenz enthält. Sie wird als Differenzengleichung n-ter Ordnung bezeichnet, wenn die höchste Ordnung der in ihr vorkommenden Differenzen dem Wert n entspricht. Sie findet u.a. Verwendung beim Euler-Verfahren. Mit Hilfe derartiger Gleichungen können Änderungen von Zustandsgrößen in Abhängigkeit der Zeit beschrieben werden. Im Gegensatz zu Differentialgleichungen werden hierbei lediglich die Übergänge vom Zeitpunkt t zum Zeitpunkt t+Δt betrachtet.
 
 

 

 

Bei Wahl des Registerblatts DGL 1. Ordnung ermittelt dieses Unterprogramm die Lösungskurve y = y(x) einer Differentialgleichung erster Ordnung vom Typ dy/dx = y' = f(x,y) durch die Verwendung des Verfahrens nach Runge-Kutta, welches im Verhältnis zum Eulerschen Streckenzugverfahren eine höhere Stabilität aufweist, da es durch die Verwendung einer automatischen Schrittweitensteuerung versucht, auftretende Rundungsfehler möglichst klein zu halten.

 

Das Programm verwendet die in den Eingabefeldern x0 = und y0 = festgelegten Startwerte zur Durchführung der Berechnungen und zur Ausgabe der grafischen Darstellung.
 

Wenden Sie die nachfolgend geschilderte Vorgehensweise an, um die Lösungskurve einer Differenzialgleichung 1. Ordnung ermitteln und grafisch ausgeben zu lassen:
 

1. Definieren Sie die zu analysierende Gleichung, gemäß den geltenden Syntaxregeln, in dem dafür vorgesehenen Eingabefeld dy/dx =.
    
2. Tragen Sie in die Felder x0 = sowie y0 = die entsprechenden Startwerte (Anfangswerte) ein und legen Sie im Eingabefeld Bereich von x0 bis x1 = einen Maximalwert für x1 fest, über welchen die Ergebnisse numerischer Berechnungen ausgegeben werden sollen.
    
3. Legen Sie mittels dem zur Verfügung stehenden Rollbalken (Anz. Schritte) die Anzahl der bei Berechnungen durchzuführenden Schritte fest.
    
4. Bedienen Sie die Schaltfläche Berechnen.
    
5. Um sich die Lösungskurve grafisch ausgeben zu lassen, bedienen Sie hierauf die Schaltfläche Darstellen.
    
6. Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters mit der Bezeichnung Nur Bereich darstellen bzw. Vollständig darstellen, ob die Lösungskurve über den gesamten Darstellungsbereich ausgegeben werden soll, oder lediglich innerhalb des festgelegten Intervallbereichs x0 < x < x1.
   
   Wurde der Kontrollschalter mit der Bezeichnung Nur Bereich darstellen gewählt, so legen Sie durch die Aktivierung des Kontrollkästchens Bereich markieren fest, ob bei der Darstellung der Lösungskurve eine Markierung des gewählten Intervallbereichs erfolgen soll.

 
Hinweis:

Die Auflösungsgenauigkeit bei Ausgabe der grafischen Darstellung hängt von der gewählten Schrittanzahl zur numerischen Ermittlung der Lösungen ab. Je höher diese gewählt wird, desto exakter wird der Funktionsverlauf ausgegeben.

 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
 
Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.
  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

 

Wird das Registerblatt Verfahrensvergleich gewählt, so ermöglicht es das Programm, die Lösungen von Differentialgleichungen 1. Ordnung mit Hilfe der folgenden Verfahren numerisch ermitteln zu lassen:
 

• Runge-Kutta-Verfahren
• Heun-Methode (Heun-Verfahren)
• Euler-Methode (Euler-Verfahren)

Um zwei dieser Methoden zu vergleichen, gehen Sie folgendermaßen vor:
 

1. Definieren Sie die, gemäß den geltenden Syntaxregeln formulierte, Differentialgleichung 1. Ordnung im Eingabefeld mit der Bezeichnung dy/dx =.
    
2. Tragen Sie in die Felder x0 = sowie y0 = die entsprechenden Startwerte (Anfangswerte) ein und legen Sie im Eingabefeld Bereich von x0 bis x1 = einen Maximalwert für x1 fest, über welchen die Ergebnisse ausgegeben werden sollen.
    
3. Wählen Sie zwei (zu vergleichende) Verfahren aus den aufklappbaren Boxen.
    
4. Legen Sie mittels dem zur Verfügung stehenden Rollbalken (Anz. Schritte) die Anzahl der bei Berechnungen durchzuführenden Schritte fest.
    
5. Bedienen Sie die Schaltfläche Berechnen. Die ermittelten Werte werden in den Tabellen ausgegeben.

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

DGL n-ter Ordnung

DGL–Gleichungssystem

Richtungsfelder DGL - Interaktiv

 

Wird die Differentialgleichung y' = dy/dx = y+e^x analytisch gelöst, so ergibt sich die Funktionsschar y = (x+1)·e^x·C.

Vorgehensweise:

Wählen Sie das Registerblatt DGL 1. Ordnung, um die Lösungen dieser DGL im Intervall 0  ≤ x ≤ 1 numerisch ermitteln zu lassen und definieren Sie die Differentialgleichung dy/dx = y+e^x, indem Sie im Eingabefeld dy/dx = die Zeichenfolge Y+E^X eingeben. Geben Sie die Zahlen 0 und 1 zur Festlegung der Startwerte (Anfangswerte) in die dafür vorgesehenen Felder x0 = und y0 = ein und legen Sie im Eingabefeld Bereich von x0 bis x1 = den Wert 1 fest.

Positionieren Sie den Rollbalken Anz. Schritte auf 500, so erhalten Sie nach einer Bedienung der Schaltfläche Berechnen, für die gestellte Anfangswertbedingung y(0) = 1, folgende Ergebnisse (Auszug).
 

X	Y
0	1,0000
0,1	1,21569
0,2	1,46368
0,3	1,75482
0,4	2,08855
0,5	2,47308
0,6	2,91539
0,7	3,42388
0,8	4,00597
0,9	4,67324
1,0	5,43656

Wie zu erkennen ist, entsprechen diese numerisch ermittelten Werte denen, welche die analytisch ermittelte Funktion y = (x+1)·e^x in diesem Bereich besitzt, sehr gut.
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Verfahrensvergleich - Beispiel 1


Verfahrensvergleich - Beispiel 2

    
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
  

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Differentialgleichung zu finden.

 

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
 

 

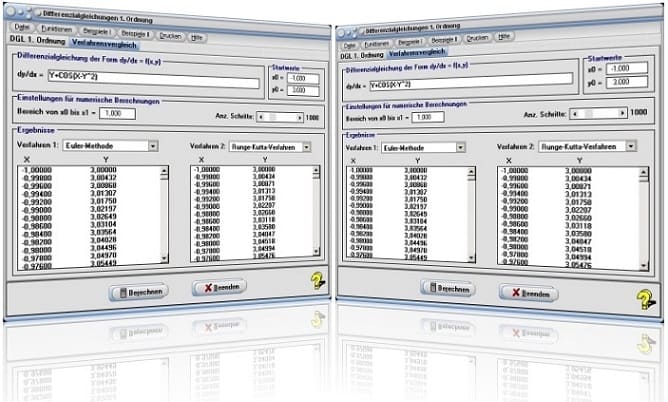
Startfenster des Unterprogramms Differentialgleichungen 1. Ordnung
 

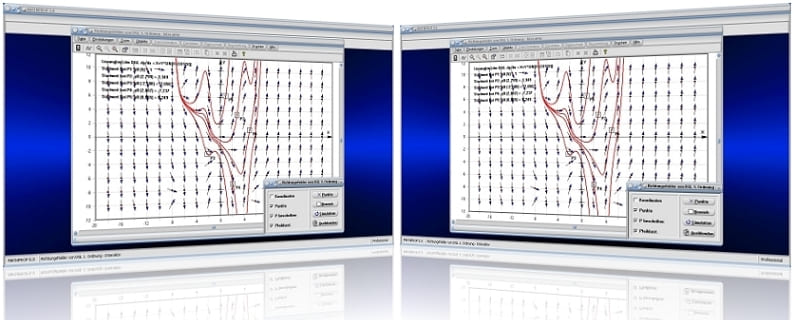
MathProf 5.0 - Unterprogramm Richtungsfelder von Differentialgleichungen 1. Ordnung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---