MathProf - Brüche - Regeln - Bruch - Verhältnisgleichung

Fachthema: Rechnen mit Brüchen
MathProf - Algebra - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Grundschule, Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung von Bruchrechnungen mit echten Brüchen und unechten Brüchen unter Festlegung von Zähler (Dividend) und Nenner (Divisor).
Nach Durchführung einer Bruchrechnung gibt das Programm das entsprechende Ergebnis sowohl in Form von Bruchzahlen wie auch als Dezimalzahl aus und ermittelt das Verhältnis der entsprechenden Zahlen.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte I zu diesem Modul:Bruchrechnen - Bruchrechnung - Bruch - Rechnen - Brüche - Bruchrechner - Regeln - Rechenregeln - Rechengesetze - Kehrbruch - Kürzen von Brüchen - Bruchteil - Bruchterme - Bruchrechnungen - Bruchrechenregeln - Kehrwert - Hauptnenner - Gemischte Zahlen - Gemischte Zahl - Gemischter Bruch - Gemischte Brüche - Schreibweise - Gemischte Schreibweise - Kürzungszahl - Zahl - Zahlen - Als Bruch - Mal - Durch - Plus - Minus - Brüche addieren - Rechnen mit Brüchen - Brüche subtrahieren - Brüche multiplizieren - Brüche dividieren - Brüche kürzen - Umwandeln von Brüchen - Bruch in Dezimalzahl - Gemeinsamer Nenner - Gemeinsamer Teiler - Gemeinsame Nenner - Echter Bruch - Unechter Bruch - Grunddarstellung - Umwandeln - Addieren - Subtrahieren - Multiplizieren - Dividieren - Zeichen - Bruch als Dezimalzahl - Dezimalschreibweise - Grundlagen - Einführung - Ergebnis - Begriff - Begriffe - Erklärung - Einfach erklärt - Übersicht - Beschreibung - Definition - Grundaufgaben - Addition von Brüchen - Subtraktion von Brüchen - Addieren von Brüchen - Subtrahieren von Brüchen - Multiplizieren von Brüchen - Dividieren von Brüchen - Dividend - Divisor - Division von Brüchen - Doppelbruch - Doppelbrüche - Doppelter Bruch - Rechenweg - Bruchregeln - Wertgleiche Brüche - Bruch durch Bruch - Bruch mal - Bruch durch - Bruch plus - Teilen - Brüche als Dezimalzahl - Bruch umrechnen - Brüche umrechnen - Ungleichnamige Brüche - Gleichnamige Brüche - Brüche gleichnamig machen - Gleichwertige Brüche - Negativer Bruch - Stammbruch - Herleitung - Ergebnis - Beweis - Echte Brüche - Unechte Brüche - Scheinbruch - Scheinbrüche - Bruchdarstellung - Brüche vereinfachen - Brüche mit Potenzen - Termumformung - Multiplikation von Brüchen - Gebrochene Zahlen - Terme - Veranschaulichen - Gleiche Nenner - Ordnen - Sortieren - Finden - Vereinfachen - Vereinfacht - Anwendungsbeispiele - Darstellen - Darstellung - Kommazahlen - Ganze Zahlen - Bruchteile - Addition - Subtraktion - Multiplikation - Division - Mehrere Brüche - Zwei Brüche |
Themen und Stichworte II zu diesem Modul:Brüche teilen - Summe - Summen - Summieren - Quotient - Faktor - Bruchzahlen - Bruchzahl - Dezimalzahl - Dezimal - Grundlagen - Grundlegendes - Wandeln - Wandlung - Umwandlung - Berechnen - Rechner - Berechnung - Kürzungszahl - Ergebnis - Übersicht - Mathe - Mathematik - Verhältnisse - Zahl - Zahlen - Teil - Teilen - Teiler - Null - Ein Ganzes - Ein - Eins - Zwei - Drei - Vier - Fünf - Sechs - Sieben - Acht - Neun - Zehn - Elf - Zwölf - Dreizehn - Vierzehn - Fünfzehn - Sechzehn - Siebzehn - Achtzehn - Neunzehn - Zwanzig - Dreißig - Vierzig - Fünfzig - Sechzig - Siebzig - Achtzig - Neunzig - Hundert - Tausend - 0 - 1 - 2 - 3 - 4 - 5 - 6 -7 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 -19 - 20 - 1/2 - 1/3 - 1/4 - 1/5 - 1/6 - 1/7 - 1/8 - 1/9 - 1/10 - 2/3 - 2/4 - 2/5 - 2/6 - 2/7 - 2/9 - 3/4 - 3/5 - 3/7 - 3/8 - 4/5 - 4/7 - 4/9 - 5/6 - 5/7 - 5/8 - 5/9 - 6/7 - 7/8 - 8/9 - 3/10 - 4/10 - 5/10 - 6/10 - 7/10 - 8/10 - 9/10 - * - / - + - Ein Halb - Ein Drittel - Ein Viertel - Ein Fünftel - Ein Sechstel - Ein Siebtel - Ein Achtel - Ein Zehntel - Zwei Zehntel - Drei Zehntel - Vier Zehntel - Fünf Zehntel - Sechs Zehntel - Sieben Zehntel - Acht Zehntel - Neun Zehntel - Zwei Drittel - Drei Viertel - Vier Fünftel - Sechs Siebtel - Sieben Achtel - Acht Neuntel - Hälfte - Drittel - Viertel - Fünftel - Sechstel - Achtel - Zehntel - Ganze - Halbe - Drittel - Viertel - Fünftel - Sechstel - Siebtel - Achtel - Neuntel - Zehntel - Zwei Viertel - Zwei Fünftel - Zwei Sechstel - Zwei Siebtel - Zwei Achtel - Zwei Neuntel - Ein Zehntel - Zwei Zehntel - Drei Zehntel - Vier Zehntel - 1 Zehntel - 2 Zehntel - 3 Zehntel - 4 Zehntel - Ein Hundertstel - Zwei Hundertstel - Drei Hundertstel - Vier Hundertstel - 1 Hundertstel - 2 Hundertstel - 3 Hundertstel - 4 Hundertstel - Halbieren - Dritteln - Mal - Geteilt - Geteilt durch - Dividiert durch - Multpliziert mit - Dividiert - Addiert - Subtrahiert - Gleicher Nenner - Dividieren mit Rest - Division mit Rest - Suchen - Finden - Rechenhilfen - Rechenhilfe - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Bruchaufgabe - Bruchaufgaben - Wie viel - Wie viele - Wieviel - Wieviele - Wie - Welche - Welcher - Welches - Wodurch - Weshalb - Was ist - Warum - Was sind - Bedeutung - Was bedeutet - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Verhältnis - Brüche vergleichen - Gleiche Brüche - Äquivalenzumformungen - Zehnerbruch - Dezimalbruch - Zehnerbrüche - Dezimalbrüche - Proportion - Proportionen - Verhältnisgleichung - Verhältnisgleichungen - Verhältnisrechnung - Verhältnis berechnen - Produktgleichung - Bruchterme kürzen - Bruchterme addieren - Bruchterme multiplizieren - Bruchterme dividieren - Bruchterme subtrahieren - Erweiterungszahl - Erweiterungsfaktor - Bruch erweitern - Erweitern von Brüchen - Erweitern - Erweitert - Auflösen - Brüche erweitern - Bruch kürzen - Kürzen - Bruch mit Wurzel - Bruch mit Hochzahl - Bruch mit Exponent - Brüche mit Wurzeln - Brüche mit Hochzahlen - Brüche mit Exponenten - Malnehmen - Multipliziert - Dividiert - Radizieren - Teilung - Verfielfachen - Verfielfachung - Bruchschreibweise - Bruchstrich - Summe - Bruchterm - Gekürzt - Gekürzter Bruch - Nenner bestimmen - Quotienten - Bruch hoch - Potenzen - Potenz - Brüche potenzieren - Stammbrüche - Gleichnamig - Ungleichnamig - Bestimmen - Bestimmung - Lösungsweg - Prozent - Prozent in Bruch - Bruch in Prozent - Brüche in Prozent - Trainer - Trainieren - Umrechnen - Umformen - Umformung - Umformungsregeln - Vereinfachung - Anteil - Anteile - Anteile berechnen - Anteil berechnen - Anteil in Prozent - Wandeln - Wandlung - Hundertstel - Bruch umschreiben - Brüche umschreiben - Brüche ordnen - Größenvergleich - Mit x - Bruchgleichungen - x - Bruchgleichung lösen - Bruchgleichung - Bruchrechenaufgaben - Negative Brüche - Brüche mit Variablen - Über Kreuz multiplizieren - Bruch mit Variablen - Brüche mit Unbekannten - Hauptnenner bestimmen - Rational machen - Rationalisieren - Brüche rationalisieren - Nenner rational machen - Merksatz - Merksätze - Definitionsmenge - Lösungsmenge |
Bruchrechnung - Verhältnis
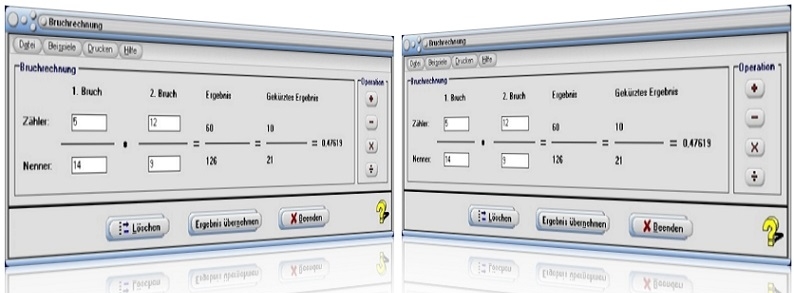
Modul Bruchrechnung
Mit Hilfe des kleinen Unterprogramms [Algebra] - Bruchrechnung lassen sich Operationen mit gemeinen Brüchen durchführen.

Grundlegendes
Das Bruchrechnen (die Bruchrechnung) zählt zum Themenbereich der analytischen Arithmetik und bezeichnet das Rechnen mit Brüchen in der Zähler-Bruchstrich-Nenner-Schreibweise.
Brüche entstehen bei der Teilung eines Ganzen oder mehrerer Ganzer. Der Zähler eines Bruchs gibt die Anzahl geteilter Ganzer an. Sein Nenner gibt Auskunft darüber in wie viele Teile ein Ganzes zu teilen ist. Der waagerechte oder schräge Strich eines Bruchs trägt die Bezeichnung Bruchstrich. Die Zahl unter dem Bruchstrich wird als Nenner bezeichnet und die Zahl über dem Bruchstrich wird mit dem Begriff Zähler benannt. Brüche werden auch als gebrochene Zahlen bezeichnet.
Stammbruch: Brüche die einen Zähler 1 besitzen heißen Stammbrüche.
Ist der Nenner eines Bruchs gleich dem Zähler eines anderen oder umgekehrt, so handelt es sich um reziproke Brüche (z.B. ist 5/4 reziprok zu 4/5). Brüche mit gleichen Nennern heißen zueinander gleichnamig. Besitzen sie hingegen unterschiedliche Nenner so werden sie als ungleichnamig bezeichnet.
Ein Bruch kann auf unterschiedliche Weise dargestellt werden:
- in Form einer mathematischer Notation (z.B. 3/4)
- in Worten (z.B. drei Viertel)
- als der Teil einer Reihe von Gegenständen
- grafisch, beispielsweise in Form des Teils eines Balkens oder eines Kreises
Bruchterme: Mit dem Begriff Bruchterm wird ein Term bezeichnet, der aus einem oder mehreren Brüchen besteht und die entsprechende Variable in wenigstens einem Nenner der Terme vorkommt.
Grunddarstellung: Als Grunddarstellung eines Bruchs (Darstellung als Bruch) wird die Darstellungsform dessen bezeichnet, wenn dieser so weit wie möglich gekürzt wurde.
Der Hauptnenner mehrerer Brüche ist das kleinste gemeinsame Vielfache der Nenner dieser Brüche. Dieser wird auch als gleicher Nenner oder gemeinsamer Nenner bezeichnet.
Kürzungszahl: Die Zahl, mit welcher ein Bruch gekürzt wird, wird als Kürzungszahl bezeichnet.
Programmbedienung
Wandlung von Bruch in Dezimalzahl (Brüche in Dezimalzahlen umwandeln):
Dieses Modul beinhaltet einen Bruchrechner und ermöglicht neben der Durchführung verschiedener Operationen mit Brüchen das Umwandeln von Brüchen in Dezimalzahlen (Dezimalschreibweise) bzw. Kommazahlen sowie das Lösen einfacher Bruchaufgaben. Bei dessen Nutzung können zwei Brüche oder aufeinanderfolgend mehrere Brüche addiert, subtrahiert, multipliziert, dividiert sowie gekürzt werden.
Brüche als Dezimalzahl - Bruch umrechnen (Brüche umrechnen): Das Programm gibt das Ergebnis einer durchgeführten Bruchoperation in Form eines gemeinen Bruchs, wie auch in gekürzter Form aus. Zudem wird dieses als Dezimalwert angezeigt.
Gehen Sie folgendermaßen vor, um Berechnungen mit gemeinen Brüchen durchzuführen:
- Geben Sie die ganzzahligen Werte für Zähler und Nenner des ersten Bruchs in die Felder 1. Bruch ein.
- Führen Sie dies ebenfalls für den zweiten Bruch durch. Legen Sie die entsprechenden Werte hierbei in den Feldern 2. Bruch fest.
- Bedienen Sie eine dafür vorgesehene Symbolschaltfläche +, -, * oder / um die gewünschte Operation mit den definierten Brüchen durchführen zu lassen.
- Möchten Sie das Ergebnis zur Ausführung weiterer Rechenoperationen verwenden, so bedienen Sie die Schaltfläche Ergebnis übernehmen. Hierbei wird das Resultat der zuletzt durchgeführten Operation in die Eingabefelder des ersten Bruchs übernommen und die Einträge in den Feldern des zweiten Bruchs werden gelöscht.
Vor Durchführung einer neuen Berechnung bedienen Sie die Schaltfläche Löschen.
Übersicht über die Zuordnung der zur Verfügung stehnden Schalter bzgl. derer auszuführender Operationen:
| Schaltersymbol | Operation |
| + | Addition |
| - | Subtraktion |
| * | Multiplikation |
| / | Division |
Hinweise:
Sind nicht alle Eingabefelder mit Zahlenwerten belegt, so wird keine Operation durchgeführt. Bei einem echten Bruch ist der Nenner größer dem Zähler. Bei einem unechten Bruch ist der Zähler größer oder gleich dem Nenner.
Beispiel zum Umgang mit diesem Modul
Nach einer Eingabe der Werte für:
1. Bruch: 5 / 9
2. Bruch: 7 / 8
werden nach der Bedienung der entsprechenden Schaltflächen nachfolgend aufgeführte Berechnungen durchgeführt und Ergebnisse ausgegeben:
| Schalter: + (Addition): Operation: 5 / 9 + 7 / 8 = 103 / 72 = 1,403556
|
| Schalter: - (Subtraktion): Operation: 5 / 9 - 7 / 8 = -23 / 72 = -0,319444
|
| Schalter: * (Multiplikation): Operation: 5 / 9 * 7 / 8 = 35 / 72 = 0,48611
|
| Schalter: / (Division): Operation: 5 / 9 / 7 / 8 = 40 / 63 = 0,634291 |

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4

Beispiel 5

Beispiel 6

Beispiel 7

Beispiel 8

Beispiel 9
Brüche - Regeln - Rechenregeln - Rechengesetze - Grundlagen - Übersicht - Rechenweg
Nachfolgend wird auf die Grundlagen der Bruchrechnung eingegangen. Hierbei werden unter anderem die hierfür geltenden Regeln bzw. Rechengesetze (auch als Rechenregeln, Bruchrechenregeln oder Bruchregeln bezeichnet) behandelt. Auch wird bei relevanten Zusammenhängen der entsprechende zu durchlaufende Rechenweg aufgezeigt.
1. Addition von Brüchen
(Addieren von Brüchen - Brüche addieren - Bruchterme addieren)
I - Brüche addieren - Allgemein:
Brüche werden addiert, indem man sie auf den gleichen Nenner (Hauptnenner) erweitert, hierauf deren Zähler addiert und den gemeinsamen Nenner (gemeinsamen Quotient) beibehält (Nenner bestimmen). Diese Vorgehensweise wird auch als Hauptnenner bestimmen bezeichnet.
Beispiel:
2/3 + 1/5
Hauptnenner: 3 · 5 = 15
Addition der Zähler: 5 · 2/15 + 3 · 3/15 = 10/15 + 9/15 = 19/15
→ 2/3 + 1/5 = 19/15 = 1 + 4/5
II - Gleichnamige Brüche addieren:
Gleichnamige Brüche werden addiert, indem die Zähler unter Beibehaltung des Nenners addiert.
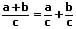
oder:
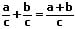
Beispiele:
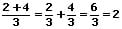
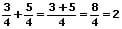
III - Ungleichnamige Brüche addieren:
Ungleichnamige Brüche werden addiert, indem man sie gleichnamig macht und hierauf wie bei gleichnamigen Brüchen die Zähler unter Beibehaltung des Nenners addiert.
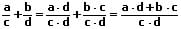
Beispiel:
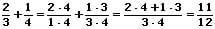
2. Subtraktion von Brüchen
(Subtrahieren von Brüchen - Brüche subtrahieren - Bruchterme subtrahieren)
I - Brüche subtrahieren - Allgemein:
Brüche werden subtrahiert, indem man sie auf den gleichen Nenner (Hauptnenner) erweitert, hierauf deren Zähler addiert und den gemeinsamen Nenner (gemeinsamen Quotient) beibehält.
Beispiel:
2/3 - 1/5
Hauptnenner: 3 · 5 = 15
Subtraktion der Zähler: 5 · 2/15 - 3 · 3/15 = 10/15 - 9/15 = 1/15
→ 2/3 - 1/5 = 1/15
II - Gleichnamige Brüche subtrahieren:
Gleichnamige Brüche werden subtrahiert, indem die Zähler unter Beibehaltung des Nenners subtrahiert.
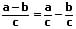
oder:
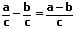
Beispiele:
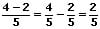
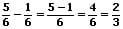
III - Ungleichnamige Brüche subtrahieren:
Ungleichnamige Brüche werden subtrahiert, indem man sie gleichnamig macht und hierauf wie bei gleichnamigen Brüchen die Zähler unter Beibehaltung des Nenners subtrahiert.
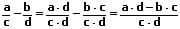
Beispiel:
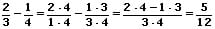
3. Multiplikation von Brüchen mit einer natürlichen Zahl (Faktorisieren)
Brüche werden mit einer natürlichen Zahl (ganzen Zahl) multipliziert (faktorisiert), indem man deren Zähler mit der natürlichen Zahl (ganzen Zahl) multipliziert. Der Nenner dieses Bruchs bleibt gleich. Dieser Vorgang wird auch als das Faktorisieren oder als Verfielfachung (das Verfielfachen) eines Bruchs bezeichnet.
Anders formuliert gilt für eine ganze Zahl (ganze Zahlen) in diesem Fall: Ein Bruch wird mit einer ganzen Zahl multipliziert, indem der Zähler des Bruches mit dieser Zahl multipliziert wird und dessen Nenner beibehalten wird.
Beispiel:
4 · 5/7 = 4 · 5/7 = 20/7
→ 4 · 5/7 = 20/7
4. Multiplikation von Brüchen mit Brüchen
(Multiplizieren von Brüchen - Brüche multiplizieren - Bruchterme multiplizieren)
Brüche werden mit Brüchen multipliziert, indem man die jeweiligen Zähler und und die jeweiligen Nenner miteinander multipliziert (Ausmultiplizieren).
Beispiel:
4/3 · 2/5
Multiplikation der Zähler: 4 · 2 = 8
Multiplikation der Nenner: 3 · 5 = 15
Ergebnis: 8/15
→ 4/3 · 2/5 = 8/15
5. Division eines Bruchs durch eine natürliche Zahl
Brüche werden durch eine natürliche Zahl dividiert, indem man den Nenner des Bruchs mit der natürlichen Zahl multipliziert und den Zähler beibehält. Als Quotienten werden die Ergebnisse durchgeführter Divisonen zweier (oder mehrerer) Zahlen bezeichnet. Werden zwei Zahlen durcheinander dividiert, so ergibt sich als Ergebnis der Quotient dieser beiden Zahlen.
Dividieren mit Rest: Bei einer Division mit Rest wird berechnet, wie oft der Divisor in den Dividend passt. Das Ergebnis ist der Quotient und der Rest (Modulo).
Beispiel:
1/4 geteilt durch 3
Zähler: 1
Multiplikation der Nenner: 4 · 3 = 12
Ergebnis: 1/12
→ 1/3 : 3 = 1/12
6. Division eines Bruches durch einen Bruch
Dividieren von Brüchen - Brüche dividieren - Brüche teilen - Bruchterme dividieren - Doppelbruch
Brüche dividieren - Brüche teilen: Brüche werden durch einen Bruch dividiert, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruches (dem Kehrbruch) multipliziert. Dies bedeutet: Im zweiten Bruch werden Zähler und Nenner vertauscht. Hierauf werden die beiden Brüche miteinander multipliziert. Dieses Verfahren wird als über Kreuz multiplizieren bezeichnet.
Doppelbruch (doppelter Bruch): Doppelbrüche liegen vor, wenn im Zähler oder Nenner eines Bruchs nochmals ein oder mehrere Brüche auftreten. Bruchterme dividieren: Durch einen Bruchterm wird dividiert, indem man diesen mit seinem Kehrwert multipliziert.
Beispiel:
2/3 geteilt durch 3/4
Kehrwert des zweiten Bruchs (Kehrbruch): 4/3
Multiplikation des ersten Bruchs mit dem Kehrwert des zweiten Bruchs:
2/3 · 4/3
Multiplikation der Zähler: 2 · 4 = 8
Multiplikation der Nenner: 3 · 3 = 9
Ergebnis: 8/9
→ 2/3 geteilt durch 3/4 = 8/9
7. Potenzieren von Brüchen
(Brüche mit Potenzen - Brüche mit Hochzahlen - Brüche mit Exponenten)
Bruch mit Hochzahl (Bruch mit Exponent): Als Brüche mit Hochzahlen (Brüche mit Potenzen oder Brüche mit Exponenten) werden Brüche bezeichnet, die einen Exponenten besitzen.
Brüche potenzieren: Brüche werden mit einem Exponenten potenziert, indem man Zähler und Nenner getrennt mit dem Exponenten multipliziert.
Beispiel:
2/3 hoch 3
Zähler: 2
Nenner: 3
Potenzierung des Zählers: 2^3 = 2 · 2 · 2 = 8
Potenzierung des Nenners: 3^3 = 3 · 3 · 3 = 27
Ergebnis: 8/27
→ (2/3)^3 = 8/27
Echter Bruch - Unechter Bruch - Natürliche Zahlen - Gemischte Zahlen - Dezimalbruch - Sachverhalte - Übersicht
1. Echte Brüche:
Echter Bruch: Ist bei einem Bruch der Zähler kleiner als der Nenner, so handelt es sich um einem echten Bruch.
Beispiele für echte Brüche:
1/4
2/9
2. Unechte Brüche:
Unechter Bruch: Ist bei einem Bruch der Nenner kleiner als der Zähler, so handelt es sich um von einem unechten Bruch.
Beispiele für unechte Brüche:
7/3
11/4
3. Scheinbrüche:
Scheinbruch: Besitzt ein Bruch als Wert eine ganze Zahl, so wird er als Scheinbruch bezeichnet.
Beispiele für Scheinbrüche:
4/2 → 2
9/3 → 3
4. Bruchzahlen - Wertgleiche Brüche:
Zahlen, welche durch Brüche angegeben werden können, heißen Bruchzahlen. Eine Bruchzahl kann durch unterschiedliche wertgleiche Brüche angegeben werden. Wertgleiche Brüche können erstellt werden, indem Zähler und Nenner eines Bruchs mit der selben Zahl multipliziert werden.
Beispiele für wertgleiche Brüche:
1/2 = 2/4 = 4/8
1/3 = 3/9 = 5/15
5. Natürliche Zahlen:
Ist der Zähler ein Vielfaches des Nenners, so stellt der Bruch eine natürliche Zahl dar.
Beispiele für natürliche Zahlen:
8/4 = 2
15/3 = 5
6. Gemischte Zahlen (gemischte Brüche - Bruch umschreiben):
Eine gemischte Zahl besteht aus einer ganzen Zahl sowie einem Bruch. Eine gemischte Zahl wird auch gemischter Bruch genannt. Diese Darstellungsform trägt auch die Bezeichnung gemischte Schreibweise. Ein gemischter Bruch liegt vor, nachdem die Aufteilung eines unechten Bruchs in einen ganzzahligen Anteil und einen echten Bruchanteil erfolgt. Alle unechten Brüche, die keine Scheinbrüche sind, lassen sich als gemischte Brüche darstellen.
Beispiele für gemischte Zahlen (gemischte Brüche):
4 2/5 = 4 + 2/5
6 2/7 = 6 + 2/7
Die Umwandlung einer gemischten Zahl in einen Bruch erfolgt, indem die ganze Zahl mit dem Nenner des Bruchs multipliziert wird und dieses Zwischenergebnis hierauf zum Zähler des Bruchs addiert wird. Der Nenner des Bruchs bleibt erhalten und das Resultat dieser Umwandlung ergibt den neuen Zähler dieses Bruchs.
Beispiele zur Umwandlung einer gemischten Zahl in einen Bruch:
5 2/9 = 5 + 2/9 = 5 · 9/9 = 35/9 + 2/9 = 37/9
1 3/7 = 1 + 3/7 = 1 · 7/7 = 7/7 + 3/7 = 10/7
7. Kehrwert eines Bruchs:
Der Kehrwert eines Bruchs (reziproker Bruch) ist ein Bruch, bei welchem dessen Zähler und Nenner veratuscht werden.
Beispiel:
Gegebener Bruch: 2/7
Sein Kehrwert lautet: 7/2
8. Negativer Bruch:
Negative Brüche: Ein negativer Bruch ist ein Bruch bei welchem entweder der Zähler oder der Nenner desselben ein negatives Vorzeichen (Minus) besitzt. Sind Zähler wie auch Nenner eines Bruchs negativ, so ist sein Wert positiv. Ist lediglich sein Zähler oder sein Nenner negativ und besitzt der andere Teil dessen ein umgekehrtes Vorzeichen, so ist der Wert des Bruchs negativ.
9. Umwandlung einer gemischten Zahl in einen Bruch:
Vorgehensweise: Die ganze Zahl wird mit dem Nenner des Bruchs multipliziert und zum Zähler des Bruchs addiert. Der Nenner dessen bleibt erhalten.
Beispiel für die Umwandlung einer gemischten Zahl in einen Bruch:
Gemischte Zahl: 5 3/7
Zähler 3 wird mit ganzer Zahl 5 multipliziert: 5 · 3 = 15
Nenner 7 bleibt erhalten
Hieraus folgt: 5 3/7 = 5 · 3/7 = 15/7
Hinweis:
Eine gemischte Zahl wird auch als gemischter Bruch bezeichnet bzw. als gemischte Schreibweise.
10. Zehnerbrüche - Dezimalbrüche:
Als Dezimalbruch oder Zehnerbruch wird ein Bruch bezeichnet, dessen Nenner die Zahl 10, 100, 1000 etc. enthält.
Beispiele für Zehnerbrüche:
3/10, 7/100, 6/1000
11. Bruchteile:
Bruchteile: Bei einem Bruchteil handelt es sich um einen kleinen Teil eines Ganzen. Errechnet werden kann dieser, indem ein Ganzes durch den Nenner des Bruchteils dividiert wird und das Ergebnis hierauf mit dem Zähler des Bruchteils multipliziert wird.
Beispiel:
Es ist der Bruchteil von 3/4 eines Ganzen von 200 € zu berechnen.
1. Das Ganze wird durch den Nenner des Bruchteils geteilt:
200 € : 4 = 50 €
2. Dieses Ergebnis wird mit dem Zähler des Bruchteils multipliziert:
50 € ⋅ 3 = 150 €
Ergebnis: 3/4 von 200 € entsprechen dem Betrag von 150 €.
12. Gleichwertige Brüche:
Gleichwertige Brüche: Brüche sind genau dann gleichwertig, wenn sie in gekürzter Form dasselbe ergeben.
13. Bruchschreibweise:
Als Bruchschreibweise wird die Schreibweise eines Bruchs mit Bruchstrich bezeichnet. Sie beruht auf Leonardo von Pisa, der sie im Jahre 1228 einführte.
14. Termumformung:
Als Termumformung wird das Umformen eines Terms in einen ergebnisgleichen Term bezeichnet, bei dem sich die Gestalt eines Terms ändert, sein Wert jedoch erhalten bleibt (beibehalten wird).
Brüche kürzen - Brüche vereinfachen - Brüche erweitern - Brüche gleichnamig machen - Kürzungsregeln
1. Brüche kürzen (Brüche vereinfachen):
Bruch kürzen - Kürzen von Brüchen: Ein Bruch kann gekürzt (vereinfacht) werden, indem der Zähler sowie der Nenner dessen durch dieselbe Zahl dividiert werden. Das Resultat dieser durchgeführten Rechenoperation heißt gekürzter Bruch. Das Kürzen von Brüchen wird auch als das Vereinfachen von Brüchen bezeichnet.
Beispiel 1 - Einfacher Bruch:
Bruch: 15/25
Kürzungszahl: 5
15/25 = 15/25 : 5/5 = 3/5
Das Ergebnis dieser Operation ist ein gekürzter Bruch (vereinfachter Bruch). Dieses lautet: 3/5
Bruchterme kürzen: Einen Bruchterm zu kürzen heißt, den Zähler sowie den Nenner eines Bruchs in einem Term durch einen gemeinsamen Teiler zu teilen.
Beispiel 2 - Bruchterm:
Gegegen sei der zu kürzende Bruch: (x+1)⋅(x+2) / (x⋅(x+1))
Der zu kürzende Term sei: (x+1)
Nach Durchführung des Kürzens ergibt sich: (x+1)⋅(x+2) / (x⋅(x+1)) = (x+2)/x
In diesem Fall wurden der Nenner (x+1)⋅(x+2) sowie der Zähler x⋅(x+1) durch den Term (x+1) dividiert.
Es gilt in solch einem Fall (bei Ausführung einer Division), wenn der Term durch den gekürzt werden soll, eine Variable enthält, stets die Definitionsmenge des Terms zu berücksichtigen und ggf. neu festzulegen.
2. Bruch erweitern:
Brüche erweitern: Das Erweitern von Brüchen geschieht, indem sowohl deren Zähler, wie auch deren Nenner mit dem gleichen Faktor multipliziert werden. Diejenige Zahl, mit der ein Bruch erweitert wird, wird als Erweiterungszahl oder Erweiterungsfaktor bezeichnet.
Beispiel:
Bruch: 3/4
Erweiterungszahl: 2
3/4 = 3/4 · 2/2 = 6/8
Ergebnis (erweiterter Bruch): 6/8
3. Brüche gleichnamig machen:
Gleichnamige Brüche: Brüche sind gleichnamig, wenn sie dieselben Nenner besitzen. Ungleichnamige Brüche sind Brüche mit ungleichen Nennern.
Gleiche Nenner: Brüche werden gleichnamig gemacht, indem man sie auf denselben Nenner bringt. Dies geschieht durch das Kürzen oder Erweitern dieser. Lediglich Brüche mit gleichem Nenner sind vergleichbar und können addiert oder voneinander subtrahiert werden.
Beispiel:
Erster Bruch: 1/2
Zweiter Bruch: 1/3
Durch das Finden des Hauptnenners werden diese beiden Brüche gleichnamig gemacht. Der Haupnenner dieser beiden Brüche ist 6.
Gleichnamige Brüche: 3/6 und 2/6
→ 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Brüche vergleichen - Nennergleiche Brüche - Zählergleiche Brüche - Brüche ordnen - Sortieren
Größenvergleich - Brüche vergleichen - Brüche ordnen
Nachfolgend aufgeführt sind die Regeln um Brüche zu vergleichen und zu ordnen:
- Besitzen zwei zu vergleichende Brüche denselben Zähler (zählergleiche Brüche), so ist der Bruch mit dem kleineren Nenner der größere Bruch
- Besitzen zwei zu vergleichende Brüche denselben Nenner (nennergleiche Brüche), so ist der Bruch mit dem kleineren Zähler der kleinere Bruch
- Sind weder die Zähler noch die Nenner zweier Brüche gleich, so sind die beiden Brüche auf einen gemeinsamen Hauptnenner zu bringen (über Kreuz zu multiplizieren) und hierauf nach den zuvor aufgeführten Kriterien zu vergleichen
Beispiele I (zählergleiche Brüche):
4/3 > 4/5, da der Nenner (Zahl 3) des Bruchs 4/3 kleiner ist als der Nenner (Zahl 5) des Bruchs 4/5
4/5 < 4/3, da der Nenner (Zahl 5) des Bruchs 4/5 größer ist als der Nenner (Zahl 3) des Bruchs 4/3
Beispiele II (nennergleiche Brüche):
3/5 > 2/5, da der Zähler (Zahl 3) des Bruchs 3/5 größer ist als der Zähler (Zahl 2) des Bruchs 2/5
2/5 < 3/5, da der Zähler (Zahl 2) des Bruchs 2/5 kleiner ist als der Zähler (Zahl 3) des Bruchs 3/5
Beispiele III (Zähler und Nenner sind ungleich):
Multiplikation über Kreuz:
3/4 > 2/5, da 3 · 5 > 2 · 4 bzw. 15 > 8
4/7 < 2/3, da 4 · 3 < 2 · 7 bzw. 12 < 14
Wurzel im Zähler - Wurzel im Nenner - Brüche rational machen - Brüche rationalisieren
Nachfolgend sind Vorgehensweisen zum Umgang mit Termen aufgeführt bei denen Brüche mit Wurzeln vorkommen. Mit dem Ausdruck Bruch mit Wurzel wird ein Bruch bezeichnet, bei dem entweder in dessen Zähler oder dessen Nenner eine Wurzel vorkommt.
Nenner rational machen: Unter dem Rationalmachen (rational machen) von Brüchen wird das Beseitigen einer Wurzel aus dem Nenner eines Bruchs verstanden.
1. Wurzel im Nenner
Um eine einzeln im Nenner vorkommende Wurzel zu beseitigen und den Nenner des Bruchs rational zu machen, werden der Zähler sowie der Nenner des Bruchs mit dieser Wurzel multipliziert (erweitert). Hierauf befindet sich im Nenner des Bruchs keine Wurzel mehr.
Beispiel 1:
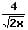
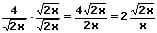
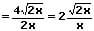
Beispiel 2:
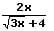
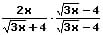
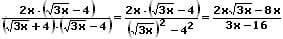
2. Wurzel im Zähler und im Nenner
Auch in diesem Fall werden der Nenner sowie der Zähler des Bruchs mit der im Nenner vorkommenden Wurzel multipliziert (erweitert).
Beispiel:
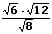
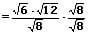
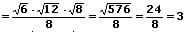
3. Zwei Wurzeln im Nenner
Befinden sich im Nenner eines Bruchs zwei Wurzeln, welche durch Additionszeichen oder Subtraktionszeichen miteinander verknüpft sind, so können diese unter bestimmten Umständen mit Hilfe des binomischen Lehrsatzes dort beseitigt werden.
Beispiel:
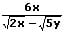
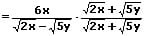
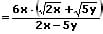
Prozentrechnung - Prozent - Wandlung Prozent in Bruch - Bruchteile
Ein Prozent entspricht einem Hundertstel.
Prozent in Bruch wandeln: Bei der Umwandlung einer Zahl mit Prozentzeichen wird dieses entfernt und die davor stehende Zahl durch 100 geteilt.
Es glit:
1% = 1/100
Beispiele:
20% = 20 · 1/100 = 20/100 = 2/10 = 1/5 = 0,2
35% = 35 · 1/100 = 35/100 = 0,35
6,7% = 6,7 · 1/100 = 67/100 = 0,67
130% = 130 · 1/100 = 130/100 = 13/10 = 1,3
Bruchteile können in Form von Brüchen, Dezimalbrüchen oder als Prozentsatz angegeben werden.
Wandlung Bruch in Prozent - Brüche umrechnen
Brüche umrechnen (Wandlung Bruch in Prozent): Ein Hundertstel entspricht einem Prozent. Bei der Umwandlung eines Bruchs in eine Zahl mit Prozentzeichen wird der Nenner des Bruchs auf die Zahl 100 gebracht und der Zähler dessen mit der Zahl vor dem Prozentzeichen multipliziert.
Es glit:
1/100 = 1%
Beispiele I:
Die Zahl 100 befindet sich im Nenner des Bruchs (Reziproke):
7/100 = 7 · 1/100 = 7%
30/100 = 30 · 1/100 = 30%
15,8/100 = 15,8 · 1/100 = 15,8%
47/100 = 47 · 1/100 = 47%
Befindet sich im Nenner des zu wandelnden Bruchs nicht die Zahl 100, so ist zuerst durch entsprechendes Erweitern oder Kürzen des Bruchs dafür zu sorgen, dass sich diese im Nenner befindet.
Beispiele II:
Die Zahl 100 befindet sich nicht im Nenner des Bruchs:
Zu wandelnder Bruch: 7/20
7/20 = (7 · 5) / (20 · 5) = 35/100 = 0,35 <- Erweiterung des Bruchs mit der Zahl 5
Zu wandelnder Bruch: 12/5
12/5 = (12 · 20) / (5 · 20) = 240/100 = 2,4 <- Erweiterung des Bruchs mit der Zahl 20
Anteil - Bruchteil - Ganzes
Anteile berechnen:
Ein Anteil kann mit Hilfe der Bruchrechnung als Bruchteil eines Ganzen berechnet werden. Hierbei wird dieser wie folgt berechnet.
Anteil = Bruchteil / Ganzes
Mittels der Kürzung bzw. Erweiterung kann der Bruch so umgeformt werden, damit sich im Nenner die Zahl 100 befindet und somit kann der Anteil in Prozent (%) ausgedrückt werden.
Beispiel:
Ein Stück Kuchen, welches 100 g Gewicht besitzt, beinhaltet 30 g Zucker. Wie hoch ist der Anteil des Zuckers in diesem Kuchenstück?
Hierdurch sind der Bruchteil (30 g) sowie das Ganze (100 g) gegeben. Durch Einsetzen der beiden entsprechenden Werte in die oben dargestellte Gleichung ergibt sich:
Anteil = 30 g / 100 g = 30/100 oder gekürzt 3/10.
Somit beträgt der Anteil des Zuckers an diesem Kuchenstück 3/10.
Nach einer Wandlung dieses Bruchs in Prozentangaben (siehe oben) kann festgestellt werden, dass der prozentuale Anteil des Zuckers in diesem Kuchestück 30 % beträgt.
Propotion - Proportionen - Verhältnisse - Verhältnisgleichung - Verhältnisrechnung
Verhältnisse (Proportionen) und Verhältnisrechnung:
Werden zwei Verhältnisse a : b und c : d zueinander in Beziehung gesetzt, so wird von einer Proportion gesprochen. Der Quotient zweier Größen wird als Verhältnis bezeichnet. Gleichungen zuvor gezeigter Art heißen Verhältnisgleichungen.
In einer Verhältnisgleichung wird durch Äquivalenzumformungen das Produkt der Außenglieder (a · d) sowie der Innenglieder (b · c) gebildet. Dieses Produkt der Außenglieder ist gleich dem Produkt der Innenglieder. Es lautet: a · d = b · c.
Eine lineare Gleichung dieser Art wird als Produktgleichung bezeichnet. Da eine dieser vier Variablen unbekannt ist, wird sie mit x bezeichnet.
Beispiel:
Das Verhältnis 8 : 5 = 4 : x sei bekannt. Durch entsprechende Umformungen wird diese Gleichung nach x aufgelöst.
8 : 5 = 4 : x
8 · x = 5 · 4
8 · x = 20
x = 20/8 = 5/2
Brüche mit Variablen - Bruchgleichungen - Bruchrechnen mit Variablen - Bruch mit Variablen - Bruchterme umformen - Termumformung
Brüche mit Variablen - Brüche mit Unbekannten: Brüche können Variablen sowohl im Zähler wie auch im Nenner enthalten. Derartige Brüche können prinzipiell gleich behandelt werden wie Brüche, welche lediglich Zahlen beinhalten. Mit ihnen kann sowohl die Addition, die Subtraktion, die Multiplikation wie auch die Division durchgeführt werden. Diese besitzen beispielsweise die nachfolgende Gestalt.
4/(2-x)
3/2bc
(5+b)/(3-ac)
Bruchgleichungen mit Variablen im Nenner
Bruchgleichungen: Häufig gilt es Gleichungen zu lösen, bei welchen sich im Nenner eines Bruchs dieser eine Variable befindet. Enthält eine Gleichung wenigstens einen Bruchterm der die Unbekannte im Nenner enthält, so wird sie als Bruchgleichung bezeichnet.
Bruchgleichung lösen: Hierbei ist zunächst zu untersuchen für welche Werte der Variable x der Nenner Null wird und die Definitionsmenge für die Variable x festzulegen (Bestimmung der Definitionsmenge). Dies kann durchgeführt werden, indem der Term jedes Nenners (Nennerterm) der Gleichung einzeln gleich Null gesetzt wird und dieser hierauf nach x aufgelöst wird (Schritt 1). Hierauf wird die entsprechende Gleichung nach x aufgelöst (Schritt 2).
Schritt 1:
Bestimmung der Definitionsmenge - Beispiel 1:
Gegeben sei die Bruchgleichung 2/x-1 = 4
Die Definitionsmenge lautet: D = R\{0}, d.h. diese Bruchgleichung ist gültig für alle Werte der Variablen x, ausschließllch der Zahl 0, denn für diese wird der Nennerterm x = 0;
Bestimmung der Definitionsmenge - Beispiel 2:
Gegeben sei die Bruchgleichung 5/(x-3) = 2
Die Definitionsmenge lautet: D = R\{3}, d.h. diese Bruchgleichung ist gültig für alle Werte der Variablen x, ausschließllch der Zahl 3, denn für diese wird der Nennerterm x-3 = 0.
Bestimmung der Definitionsmenge - Beispiel 3:
Gegeben sei die Bruchgleichung 3/(x+1) = 2/(x-2)
Die Definitionsmenge lautet: D = R\{-1;2}, d.h. Diese Bruchgleichung ist gültig für alle Werte der Variablen x, ausschließllch den Zahlen -1 und und 2, denn für diese werden die Nennerterme x+1 bzw. x-2 gleich 0.
Schritt 2:
Im folgenden Schritt wird die Gleichung mittels Termumformung nach der Variable x aufgelöst.
Auflösung nach Variable - Beispiel 1:
Gegeben sei die Bruchgleichung 2/x-1 = 4.
Um den Term x-1 im Nenner des linken Bruchs verschwinden zu lassen, werden beide Seiten der Gleichung mit (x-1) multipliziert. Es folgt:
2/x-1 = 4 | ·(x-1)
2 = 4(x-1)
4(x-1) = 2
4x-4 = 2
4x = 6
x = 6/4 = 3/2
Als Lösung der Gleichung wird für die Variable x der Wert 3/2 ermittelt. Somit lautet die Lösungsmenge dieser Bruchgleichung L = {3/2}
Auflösung nach Variable - Beispiel 2:
Gegeben sei die Bruchgleichung 3/(x+1) = 2/(x-2).
Um den Term x+1 im Nenner des linken Bruchs verschwinden zu lassen, werden beide Seiten der Gleichung mit (x+1) multipliziert. Es folgt:
3/(x+1) = 2/(x-2) | ·(x+1)
Um den Term x-2 im Nenner des rechten Bruchs verschwinden zu lassen, werden beide Seiten der Gleichung mit (x-2) multipliziert. Es folgt:
3 = 2(x-1)/(x-2) | ·(x-2)
3(x-2) = 2(x-1)
3x-6 = 2x-2 | -2x
x+6 = -2
x = -8
Als Lösung der Gleichung wird für die Variable x der Wert -8 ermittelt. Somit lautet die Lösungsmenge dieser Bruchgleichung L = {-8}
Beim Halbieren erfolgt die Zerlegung einer Menge in zwei gleich große Teile. Die beiden Hälften sind zwei exakt gleich große Mengen.
Beim Dritteln erfolgt die Zerlegung einer Menge in drei gleich große Teile. Bei allen drei Teilen handelt es sich um exakt gleich große Mengen.
Ein Halb ist die Hälfte eines Ganzen.
Ein Drittel ist der dritte Teil eines Ganzen.
Ein Viertel ist der vierte Teil eines Ganzen.
Ein Fünftel ist der fünfte Teil eines Ganzen.
Ein Sechstel ist der sechste Teil eines Ganzen.
Ein Siebtel ist der siebte Teil eines Ganzen.
Ein Achtel ist der achte Teil eines Ganzen.
Ein Zehntel ist der zehnte Teil eines Ganzen.
Werden von einer Gesamtheit zwei gleich große Stücke entnommen, so entspricht dies zwei Zehntel oder einem Fünftel dessen.
Werden von einer Gesamtheit drei gleich große Stücke entnommen, so entspricht dies drei Zehntel dessen.
Werden von einer Gesamtheit vier gleich große Stücke entnommen, so entspricht dies vier Zehntel oder zwei Fünftel dessen.
Werden von einer Gesamtheit sechs gleich große Stücke entnommen, so entspricht dies sechs Zehntel dessen oder drei Fünftel dessen.
Werden von einer Gesamtheit sieben gleich große Stücke entnommen, so entspricht dies sieben Zehntel dessen.
Werden von einer Gesamtheit acht gleich große Stücke entnommen, so entspricht dies acht Zehntel dessen.
Werden von einer Gesamtheit neun gleich große Stücke entnommen, so entspricht dies neun Zehntel dessen.
Zwei Drittel einer Gesamtheit entsprechen zwei von drei gleich großen Stücken dieser Gesamtheit.
Drei Viertel einer Gesamtheit entsprechen drei von vier gleich großen Stücken dieser Gesamtheit.
Vier Fünftel einer Gesamtheit entsprechen vier von fünf gleich großen Stücken dieser Gesamtheit.
Sechs Siebtel einer Gesamtheit entsprechen sechs von sieben gleich großen Stücken dieser Gesamtheit.
Sieben Achtel einer Gesamtheit entsprechen sieben von acht gleich großen Stücken dieser Gesamtheit.
Acht Neuntel einer Gesamtheit entsprechen acht von neun gleich großen Stücken dieser Gesamtheit.
Zwei Viertel einer Gesamtheit entsprechen zwei von vier gleich großen Stücken dieser Gesamtheit. Dies entspricht der Hälfte derer.
Zwei Fünftel einer Gesamtheit entsprechen zwei von fünf gleich großen Stücken dieser Gesamtheit.
Zwei Siebtel einer Gesamtheit entsprechen zwei von sieben gleich großen Stücken dieser Gesamtheit.
Zwei Achtel einer Gesamtheit entsprechen zwei von acht gleich großen Stücken dieser Gesamtheit. Dies entspricht einem Viertel derer.
Zwei Neuntel einer Gesamtheit entsprechen zwei von neun gleich großen Stücken dieser Gesamtheit.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Bruchrechnung zu finden.
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Zahluntersuchung

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















