MathProf - Kettenbrüche - Kommaverschiebung - Dezimalzahlen

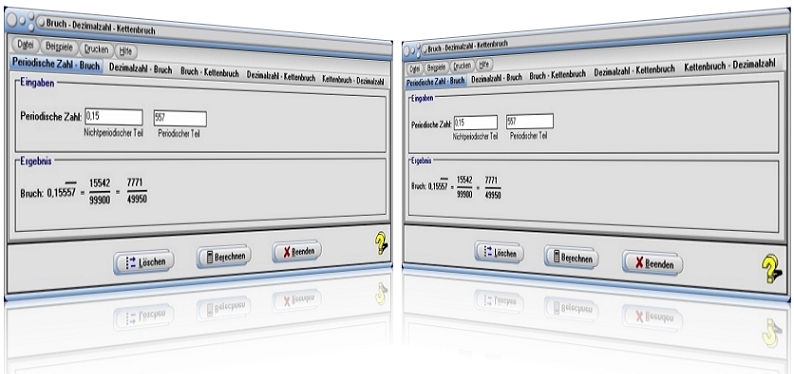
Modul Bruch - Dezimalzahl - Kettenbruch

---

 
Das kleine Unterprogramm [Algebra] -[Sonstiges] - Bruch - Dezimalzahl - Kettenbruch ermöglicht es, die verschiedenen Darstellungsformen gebrochener Zahlen ineinander umzuwandeln.
 

Folgende Umwandlungsformen stehen in diesem Modul zur Auswahl:
 

• Periode - Bruch
• Dezimalzahl - Bruch
• Bruch - Kettenbruch
• Dezimalzahl - Kettenbruch
• Kettenbruch - Dezimalzahl

 

   
Periodische Zahlen:

Es wird zwischen folgenden Arten periodischer Zahlen unterschieden:

1. Gemischt periodische Zahlen (gemischt periodische Dezimalzahlen):

Unter gemischt periodischen Zahlen werden Dezimalzahlen verstanden, bei welchen zwischen dem Komma und dem periodischen Teil nach dem Komma noch mindestens eine weitere Ziffer steht, welche nicht zur Periode zählt. Eine gemischt periodische Zahl wird auch als periodische Zahl bezeichnet.

2. Rein periodische (reinperiodische) Zahlen:

Unter rein periodischen (reinperiodischen) Zahlen werden Dezimalzahlen verstanden, bei welchen die periodische Zahlenanordnung unmittelbar nach dem Komma beginnt.

3. Periodische Dezimalzahlen:

Unter einer periodischen Dezimalzahl wird die Dezimaldarstellung einer Zahl verstanden, deren Ziffern periodisch angeordnet sind und deren sich unendlich wiederholender Teil nicht gleich dem Wert Null ist.

---

Möchten Sie eine periodische Zahl in einen gemeinen Bruch umwandeln lassen, so wählen Sie das Registerblatt Periode - Bruch, geben den nichtperiodischen, sowie den periodischen Teil der Zahl in die entsprechenden Felder ein und bedienen hierauf die Schaltfläche Berechnen.
 

Der ermittelte Bruch wird unterhalb der Eingabefelder ausgegeben und zudem in Form eines gekürzten Bruchs angezeigt. Bei Eingabe der Werte für die periodische Zahl gilt es zu beachten, dass der nichtperiodische Teil eine (positive) rationale Zahl sein kann, während der periodische Teil positiv und ganzzahlig sein muss.

Hinweis:

Der periodische Teil der zu wandelnden periodischen Zahl muss mindestens aus drei Zeichen bestehen, wobei eines dieser Zeichen ein Komma (bzw. Punkt) sein muss. Rein ganzzahlige Werteingaben werden mit einer Fehlermeldung quittiert.

 

 
Soll eine beliebige (positive) Dezimalzahl in einen Bruch gewandelt werden, so wählen Sie das Registerblatt Dezimalzahl - Bruch, geben diese in das dafür vorgesehene Feld mit der Bezeichnung Dezimalzahl ein und bedienen hierauf die Schaltfläche Berechnen.

Auch nach Ausführung dieser Berechnung wird als Ergebnis der ermittelte gemeine Bruch ausgegeben und zusätzlich in einen gekürzten Bruch umgewandelt.
 

 
Kettenbruch - Kettenbrüche - Kettenbruchentwicklung:

Kettenbrüche werden dazu verwendet, rationale Näherungen an eine vorgegebene reelle Zahl zu ermitteln (Näherungsbrüche). Diese betreffende Zahl wird mit der Hilfe von Brüchen in der Form genähert, damit Zähler und Nenner des Kettenbruchs für die erzielte Genauigkeit der Darstellung möglichst kleine Werte besitzen.

Ein Kettenbruch ist die Darstellung einer Zahl in Form einer Kette von Brüchen die stets den Zähler 1 besitzen. Jede rationale Zahl kann in einen Kettenbruch gewandelt werden und jeder Kettenbruch beschreibt wiederum eine rationale Zahl. Kettenbrüche sind fortgesetzte Brüche und stellen sich in folgender Form dar:
 

für alle a[i] mit Ausnahme a[0] gilt: a[i] > 0

Alle a[i] müssen natürliche Zahlen sein und dürfen nicht gleich der Zahl 1 sein. Als Kettenbruchentwicklung wird die Entwicklung von Brüchen zuvor beschriebener Art verstanden.

---

Um eine Zahl, die als Bruch vorliegt, in einen Kettenbruch zu wandeln, steht das Registerblatt Bruch - Kettenbruch zur Verfügung. Soll eine Zahl in Form eines Bruchs in einen Kettenbruch gewandelt werden, so geben Sie die Werte für Zähler und Nenner des Bruchs in die entsprechenden Felder ein und bedienen hierauf die Schaltfläche Berechnen. Der definierte Bruch wird zusätzlich als Dezimalzahl ausgegeben.
 

Dezimalzahlen:

Unter einer Dezimalzahl (Kommazahl) wird die Dezimaldarstellung einer Zahl verstanden. Sie ist eine Kommazahl und besteht aus Vorkommastellen sowie Nachkommastellen. Ist die Nachkommastelle keine Null, so liegt diese zwischen den Werten zweier ganzer Zahlen. Dezimalzahlen werden auch als Kommazahlen bezeichnet.
 
Abbrechende Dezimalzahlen:

Eine abbrechende Dezimalzahl besitzt endlich viele Nachkommastellen, die nicht null sind.

Dezimalzahlen vergleichen:

Die jeweilige Anzahl der Nachkommastellen zweier Dezimalzahlen wird angepasst. Dies bedeutet, dass die kürzere Zahl durch das Anhängen von Nullen (Endnullen) an die Länge der anderen Zahl angeglichen wird. Das Komma (der Separator) wird entfernt. Hierauf können die beiden Dezimalzahlen auf die sie beinhaltenden natürlichen Zahlen verglichen werden. Ein Vergleichen zweier Dezimalzahlen kann auch anhand ihrer Stellenwerte erfolgen.

Vorkommastellen - Nachkommastellen:

Dezimalzahlen (Kommazahlen) besitzen die Eigenschaft, dass sie ein Komma als Trennzeichen enthalten. Die Ziffern die sich vor dem Komma befinden, werden als Vorkommastellen und die Ziffern hinter dem Komma werden als Nachkommastellen bezeichnet.

Kommaschreibweise - Dezimalschreibweise:

Bei der Kommaschreibweise oder Dezimalschreibweise von Zahlen bestimmt die Anzahl der Stellen hinter dem Komma, ob sich im Nenner bei der Schreibweise dieser Zahlen als Bruch die Zahl 10, 100, 1000 oder 10000 etc. befindet. Die erste Stelle hinter dem Komma gibt die Anzahl der Zehntel dieser Zahl an. Die zweite Stelle bestimmt die Anzahl der Hundertstel, die dritte Zahl bestimmt die Anzahl der Tausendstel usw. dieser Zahl

Komma verschieben (Kommaverschiebung):

Bei einer Dezimalzahl entspricht eine Kommaverschiebung nach rechts der Multiplikation dieser Zahl mit einer Zehnerpotenz und eine Kommaverschiebung nach links entspricht der Division dieser Zahl durch eine Zehnerpotenz .

Wird das Komma einer Zahl nach links verschoben, so entspricht dies der Division dieser Zahl durch die Zahl 10.

Beispiele:

7000 : 10 = 700,0
700 : 10 = 70,0
70 : 10 = 7,0
7 : 10 = 0,7
0,7 : 10 = 0,07
0,07 : 10 = 0,007
0,007 : 10 = 0,0007

Wird das Komma einer Zahl nach rechts verschoben, so entspricht dies der Multiplikation dieser Zahl mit der Zahl 10.

Beispiele:

7000,0 · 10 = 70000
700,0 · 10 = 7000
70,0 · 10 = 700
7,0 · 10 = 70
0,7 · 10 = 7
0,07 · 10 = 0,7
0,007 · 10 = 0,07

---

Möchten Sie eine Dezimalzahl in einen Kettenbruch wandeln lassen, so wählen Sie das Registerblatt Dezimalzahl - Kettenbruch, definieren diese im entsprechenden Eingabefeld und bedienen hierauf die Schaltfläche Berechnen.
 

 
Wie bereits beschrieben, kann jeder Kettenbruch in eine Dezimalzahl gewandelt werden. Eine Umwandlung dieser Art können Sie durchführen lassen, indem Sie das Registerblatt Kettenbruch - Dezimalzahl wählen, den Kettenbruch im dafür vorgesehenen Eingabefeld definieren und den Schalter Berechnen bedienen.

Beachten Sie:

Die (positiven) Zahlenwerte sind, durch Semikola voneinander getrennt, einzugeben (ohne Leerzeichen).
  
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

P-adische Brüche

 

Beispiel 1 - Wandlung Periodische Zahl - Bruch:                          

Soll die periodische Zahl 0,15557 in einen Bruch umgewandelt werden, so wählen Sie das entsprechende Registerblatt, geben im linken Feld (nichtperiodischer Teil) die Zahl 0,15, im rechten Feld (periodischer Teil) die Zeichenfolge 557 ein und bedienen die Schaltfläche Berechnen.

 

Als Ergebnisse erhalten Sie den Bruch in

 

ungekürzter Form: 15542 / 99900

sowie in gekürzter Form: 7771 / 49950
 

Beispiel 2 - Wandlung Dezimalzahl - Bruch:

 

Um die Dezimalzahl 2,2415 in einen Bruch umwandeln zu lassen, wählen Sie das entsprechende Registerblatt, geben diese Dezimalzahl in das Feld Dezimalzahl ein und bedienen hierauf die Schaltfläche Berechnen. Als Resultat wird ausgegeben:

2,2415 = 2 + 2415 / 10000 = 2 + 483 / 2000.

 

Beispiel 3 - Wandlung Bruch - Kettenbruch:
 

Nach der Wahl des hierfür relevanten Registerblatts und der Eingabe der Zahlenwerte 557 und 177 in die dafür vorgesehenen Felder, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

Der Bruch 557/177 kann in Form eines Kettenbruchs ausgedrückt werden, mit: 3;6;1;4;5
 

Beispiel 4 - Wandlung Kettenbruch - Dezimalzahl:

Um den Kettenbruch 1;2;3;4;5 in eine Dezimalzahl und einen Bruch wandeln zu lassen, wählen Sie das dafür zur Verfügung stehende Registerblatt, definieren die Zeichenfolge des Kettenbruchs im dafür vorgesehenen Feld und bedienen hierauf die Schaltfläche Berechnen.

 

Das Programm ermittelt, dass sich der definierte Kettenbruch in Form einer Dezimalzahl, bzw. eines Bruchs folgendermaßen darstellen lässt:

 

Als Dezimalzahl: 1,43312102

Als Bruch: 225 / 157
 

 

Beispiel 1


Beispiel 2
 

Beispiel 3
 

Beispiel 4
 

Beispiel 5

    

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Kettenbruch zu finden.

 

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

 

MathProf 5.0 - Unterprogramm P-adische Brüche

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---