MathProf - Stauchung - Punktspiegelung - Spiegelung - Streckung

Fachthemen: Transformation - Rotation - Streckung - Spiegelung - Parallelstreckung - Symmetrie
MathProf - Geometrie - Planfiguren - Software für interaktive Mathematik. Sie eignet sich unter anderem zur Darstellung von Gebilden und zur Analyse von Sachverhalten 2. und 3. Dimension. Dieses Programm ermöglicht das Lösen verschiedenster Aufgaben und die Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen und eignet sich für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung und Analyse von geometrischen Bewegungen in der Ebene.
In diesem Teil des Programms bestehen zur Praktizierung der Transformation von Punkten frei festlegbarer regelmäßiger und unregelmäßiger Vielecke folgende Möglichkeiten:
- Geometrische Figuren verschieben (Translation)
- Geometrische Figuren drehen um einen frei definierbaren Drehpunkt
- Geometrische Figuren spiegeln an einer Symmetrieachse
- Geometrische Figuren strecken (zentrische Streckung)
- Geometrische Figuren stauchen mit Streckfaktor und Streckzentrum
- Geometrische Figuren punktspiegeln an Spiegelpunkt
- Geometrische Figuren scheren mit einem festgelegten Scherfaktor
- Geometrische Figuren an einer Gerade spiegeln
- Geometrische Figuren an Achsen spiegeln
Zudem erlaubt dieses Unterprogramm auch die interaktive Verrichtung von Untersuchungen mit geometrischen Gebilden hinsichtlich derer Kongruenz, derer Punktsymmetrie, derer Achsensymmetrie, derer Spiegelsymmetrie, derer Drehsymmetrie (Rotationssymmetrie) sowie weiterer geometrischer Eigenschaften.
Des Weiteren ermöglicht es das Berechnen der Koordinatenwerte transformierter Gebilde während dem Ablauf einer Simulation.
Die vom Rechner ausgeführten Schritte werden zur Echtzeit aktualisiert und das Programm stellt die entsprechenden Zusammenhänge unmittelbar nach Eintritt einer interaktiven Operation dar. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Streckung - Verschiebung - Translation - Drehen - Rotation - Stauchung - Geradenspiegelung - Parallelverschiebung - Punktspiegelung - Scherung - Figuren - Gebilde - Polygone - Spiegelung an einer Geraden - Geometrische Flächen - Spiegelung an der x-Achse - Verschiebung in x-Richtung - Streckung in x-Richtung - Spiegelung an der y-Achse - Verschiebung in y-Richtung - Streckung in y-Richtung - Punkte - Definition - Erklärung - Beschreibung - Spiegelung eines Punkts - Abbildungen - Punktsymmetrie zum Ursprung - Punkt spiegeln - Punkt drehen - Punkt verschieben - Am Ursprung spiegeln - Punkt - Scherungsgerade - Begriff - Begriffe - Gerade - Dreieck - Viereck - Fünfeck - Sechseck - Achteck - Zentrisch strecken - Koordinaten - Lineare Streckung - Strecke - Spiegelgerade - Spiegelpunkt - Kollinearität - Parallelität - Komplanarität - Symmetrische Figuren - Figur drehen - Figur verschieben - Figur spiegeln - Drehung um den Ursprung - Drehung in der Ebene - Verkleinern - Vergrößern - Verkleinerung - Vergrößerung - Parallel - Orthogonal - Verändern - Veränderung - Ändern - Änderung - Vertikal - Senkrecht - Waagerecht - Horizontal - Schräg - Stauchen - Strecken - Spiegeln - Schiebung - Bild - Grafik - Abbilden - Abbildung - An der x Achse gespiegelt - Gedreht - Gespiegelt - Gestaucht - Gestreckt - Abgebildet - Plotter - Rechner - Graph - Koordinaten - Bildpunkte - Herleitung - Beweis - Plotten - Bilder - Lösung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Bedeutung - Was bedeutet - Was ist - Was sind - Welche - Welcher - Welches - Wodurch - Weshalb - Warum - Erklärung - Einfach erklärt - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - 30 Grad - 45 Grad - 60 Grad - 90 Grad - 120 Grad - 270 Grad - Winkel - Drehung - Darstellung - Berechnen - Berechnung - Darstellen - Grafische Darstellung - Drehung im Koordinatensystem - Verschiebung - Koordinaten von Bildpunkten |
Bewegungen in der Ebene mit Figuren

Modul - Bewegungen in der Ebene
Der Programmpunkt [Geometrie] - Bewegungen in der Ebene ermöglicht es, Bewegungen geometrischer Objekte in der Ebene interaktiv zu analysieren. Es wird die Möglichkeit geboten Kongruenzabbildungen darzustellen und zu untersuchen.

Bewegung: Bei der Ausführung einer Bewegung sind Bild und Ausgangsfigur kongruent (deckungsgleich). Dies trifft dann zu, wenn mit der Ausgangsfigur eine Verschiebung, eine Drehung oder eine Spiegelung durchgeführt wird.
Zur Ausführung von Bewegungen bzw. Transformationen mit Polygonen stehen in diesem Modul folgende Möglichkeiten zur Auswahl:
-
Verschiebung - Translation (Verschieben)
Verschiebung eines Objekts, beschrieben durch die Punkte P1-Pn, in x- wie y-Achsrichtung, um einstellbare Werte. -
Drehung - Rotation (Drehen)
Drehung eines Objekts, beschrieben durch die Punkte P1-Pn, an Drehpunkt DP, um einstellbaren Drehwinkel (Rotationswinkel). -
Drehstreckung (Drehstrecken)
Drehung eines Objekts, beschrieben durch die Punkte P1-Pn, an Drehpunkt DP, um einstellbaren Drehwinkel und anschließender Streckung, mit einstellbarem Streckfaktor. -
Geradenspiegelung (Achsenspiegelung)
Geradenspiegelung eines Objekts, beschrieben durch die Punkte P1-Pn, an Gerade durch die Punkte GP1 und GP2. -
Zentrische Streckung / Zentrische Stauchung (Zentrisch strecken - zentrisch stauchen)
Zentrische Streckung eines Objekts, beschrieben durch die Punkte P1-Pn, mit Streckzentrum SP und Streckung, mit einstellbarem Streckfaktor. -
Punktspiegelung (Punktspiegeln)
Punktspiegelung eines Objekts, beschrieben durch die Punkte P1-Pn, an Spiegelpunkt SP. -
Verschiebung / Streckung / Stauchung (Verschieben / Strecken /Stauchen)
Verschiebung eines Objekts, beschrieben durch die Punkte P1-Pn, in x- wie y- Achsrichtung, um einstellbare Werte und anschließender Streckung (Stauchung), mit einstellbarem Streckfaktor. -
Parallelstreckung (Parallel strecken)
Parallelstreckung eines Objekts, beschrieben durch die Punkte P1-Pn, an einer Geraden durch die Punkte GP1-GP2, sowie einer Geraden durch die Punkte GP3-GP4. -
Scherung an einer Geraden (Scheren an Gerade - Schrägspiegelung)
Scherung eines Objekts, beschrieben durch die Punkte P1-Pn, an einer Geraden durch die Punkte GP1-GP2, mit einstellbarem Scherfaktor.
Geometrische Transformationen - Definition
Nachfolgend sind Erläuterungen zu grundlegenden geometrischen Transformationen zu finden.
Zentrische Streckung:
Eine zentrische Streckung ist eine Bewegung, die alle Strecken in einem bestimmten, gegebenen Verhältnis vergrößert oder verkleinert. Sie ist durch ihr Zentrum sowie einen von ihr verschiedenen Punkt eindeutig festgelegt. Alle Bildstrecken verlaufen parallel zu den jeweils ursprünglichen Strecken.
Streckung:
Eine Streckung ist eine Bewegung, bei welcher alle Winkel unverändert bleiben und sich die Längenverhältnisse der Bildstrecken um einen festen Faktor vergrößern (Proportionalitätsfaktor > 1).
Stauchung:
Eine Stauchung ist eine Bewegung, bei welcher alle Winkel unverändert bleiben und sich die Längenverhältnisse der Bildstrecken um einen festen Faktor verkleinern (Proportionalitätsfaktor < 1).
Verschiebung:
Eine Verschiebung (Parallelverschiebung, Translation oder Schiebung) ist eine Bewegung, bei welcher jeder Punkt der Bildebene, oder des Raums in dieselbe Richtung sowie um dieselbe Strecke verschoben wird.
Punktspiegelung:
Eine Punktspiegelung in der Ebene um einen Punkt P entspricht der Drehung um 180° bezüglich eines Drehzentrums P. Der Punkt P, an dem gespiegelt wird entspricht dem Schnittpunkt der Drehachse und der Spiegelebene. Er wird als Symmetriezentrum bezeichnet. Punktspiegelungen sind sowohl winkel-, längen- wie auch geradentreu.
Geradenspiegelung (Spiegelung an einer Geraden):
Eine Geradenspiegelung (Spiegelung an einer Geraden) ordnet jedem Punkt P einen Bildpunkt P' zu, welcher dadurch bestimmt ist, dass die Verbindungsstrecke [PP'] von der Gerade rechtwinklig halbiert wird.
Drehung (Rotation):
Eine Drehung um einen Punkt P in der Ebene mit einem Drehwinkel α ist eine eineindeutige Abbildung auf sich selbst. Jede Drehung verfügt über einen Fixpunkt, welcher auf sich selbst abgebildet wird. Die Ausführung einer Drehung um einen Winkel von 360° entspricht der identischen Abbildung-
Drehstreckung:
Eine Drehstreckung ist eine Ähnlichkeitsabbildung, welche sich in Form einer Kombination der beiden geometrischen Operationen Drehung und Streckung darstellen lässt.
Scherung:
Eine Scherung ist eine affine Abbildung auf sich selbst, bei welcher in der Ebene der Flächeninhalt der geometrischen Abbildung erhalten bleibt. Jeder Punkt der Achse der Geraden (Scherungsachse) an welcher die Scherung ausgeführt wird, wird auf sich abgebildet (bleibt fix). Der Abstand jedes Punktes zur Achse der Geraden bleibt unverändert.
Gleitspiegelung (Schubspiegelung):
Unter einer Gleitspiegelung (Schubspiegelung) wird eine Spiegelung an einer Geraden (Spiegelachse) verstanden, bei der die Translation parallel zur Geraden vonstatten geht.
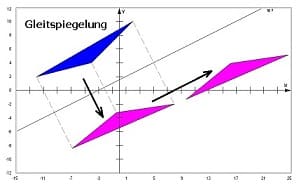
Darstellung
Um Untersuchungen zur Ausführung von Bewegungen (Transformationen) mit Polygonen durchzuführen, gehen Sie folgendermaßen vor:
-
Legen Sie zunächst fest, ob bei einem Wechsel zwischen den zur Verfügung stehenden Transformationsarten das bereits defnierte Objekt beibehalten werden soll, oder ob bei jeder Aktivierung eines Kontrollschalters zur Durchführung einer Transformation, das entsprechend vordefinierte (von Punktzahl abhängige) Objekt verwendet werden soll. Soll das momentan definierte geometrische Objekt (Ortspunktkoordinaten des Objekts) beim Wechsel zwischen den Transformationsarten beibehalten werden, so aktivieren Sie das Kontrollkästchen Punkte behalten.
-
Bestimmen Sie durch die Bedienung des Steuerelements Punktanz. die Anzahl der Punkte, mit welchen ein Gebilde erzeugt werden soll (zwischen 1 und 10).
-
Wählen Sie, durch die Aktivierung des entsprechenden Kontrollschalters, die Art der mit dem Ursprungsobjekt durchzuführenden Transformation.
-
Möchten Sie die Koordinatenwerte eines Punktes exakt festlegen, so können Sie die Schaltfläche Punkte auf dem Bedienformular nutzen und die entsprechenden Werte im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
-
Wollen Sie die Lage eines Punktes mit der Maus verändern, so klicken Sie mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich des Urprungsobjekts und bewegen den Mauscursor bei gedrückt gehaltener Maustaste.
-
Verwenden Sie die auf dem Bedienformular zur Verfügung stehenden Schieberegler (falls vorhanden), um die Parameterwerte für die entsprechende Transformation einzustellen.
-
Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die Auswahl der zu simulierenden Größe durch die Aktivierung des entsprechenden Kontrollschalters treffen. Ebenfalls können Sie hierauf ggf. die Werte für Schrittweite, Verzögerung bzw. die Anzahl zu verwendender Winkelschritte einstellen. Ändern Sie diese bei Bedarf und bestätigen Sie mit OK. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Hinweis:
Möchten Sie Zusammenhänge dieser Art ohne die Verwendung von Mausoperationen zur Erstellung von Gebilden durchführen, so steht der Menüpunkt Polygone zur Verfügung.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
-
Punkte: Beschriftung der Mausfangpunkte des aufgespannten Polygons ein-/ausschalten
-
Koordinaten: Anzeige der Koordinatenwerte der Mausfangpunkte ein-/ausschalten
-
Polygone füllen: Farbfüllung der Polygone ein-/ausschalten
-
Hilfslinien: Darstellung der Hilfslinien ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel
Mit einem Dreieck, welches durch die Punkte P1 (2 / 2), P2 (8 / 2) und P3 (2 / 6) beschrieben wird, ist eine Drehstreckung durchzuführen. Diese soll um den Drehpunkt DP (1 / -1) mit einem Winkel von 125° und einem Streckfaktor von 1,5 erfolgen.
Vorgehensweise:
Aktivieren Sie das Kontrollkästchen Punkte behalten.
Nach einer Festlegung der Punktezahl auf 3, der Positionierung des Schiebereglers Drehwinkel auf den Wert 125, der Positionierung des Schiebereglers Streckfaktor auf den Wert 1,5, der Definition der Koordinatenwerte der Punkte des Ursprungsdreiecks, sowie des Drehpunkts DP durch einen Klick auf die Schaltfläche Punkte, werden für das transformierte Dreieck folgende Koordinatenwerte ausgegeben:
P4 (-3,547 / -2,352)
P5 (-8,709 / 5,02)
P6 (-8,461 / -5,794)
Wird der Kontrollschalter Geradenspiegelung aktiviert, so führt das Programm eine Spiegelung des Dreiecks an einer Geraden durch. Zunächst verwendet es die vordefinierten Geradenpunkte GP1 (0 / 0) sowie GP2 (-2 / 9). Durch einen erneuten Klick auf die Schaltfläche Punkte können die Koordinatenwerte der Geradenpunkte verändert werden und somit Spiegelungen dieser Art an beliebigen Geraden durchgeführt werden. Die Durchführung weiterer Transformationsoperationen mit einem definierten Objekt kann nach obiger Methode beliebig oft fortgesetzt werden.
Hinweis:
Figuren heißen ähnlich zueinander, wenn deren Seiten im gleichen Verhältnis zueinander stehen und ihre Winkel dieselbe Größe besitzen.

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5

Grafische Darstellung - Beispiel 6

Grafische Darstellung - Beispiel 7

Grafische Darstellung - Beispiel 8
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Zentrische Streckung
Wikipedia - Drehstreckung
Wikipedia - Drehung
Wikipedia - Spiegelung
Wikipedia - Scherung
Wikipedia - Affine Abbildung
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
MathProf 5.0 - Unterprogramm Polygone

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















