MathProf - Arithmetische Folgen - Geometrische Folge - Folge - Reihen

Fachthemen: Arithmetische Zahlenfolgen - Geometrische Zahlenfolgen - Geometrische Reihen - Reihen
MathProf - Analysis - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Ermittlung (Bildung der Summe) und Darstellung
arithmetischer Folgen und geometrischer Folgen.
In diesem Teilprogramm erfolgt unter anderem das Berechnen der Glieder einer geometrischen Reihe unter der Anwendung der geometrischen Summenformel. Auch wird es ermöglicht, die Glieder sowie die Partialsumme einer arithmetischen Zahlenfolge oder einer geometrischen Zahlenfolge bestimmen zu lassen.
Zudem wird eine Analyse bzgl. der Konvergenz oder Divergenz einer definierten Zahlenfolge durchgeführt. Auch der ggf. vorhandene Grenzwert dieser wird bestimmt.
Nach der Durchführung einer numerischen Berechnung kann der entsprechende Sachverhalt grafisch dargestellt und analysiert werden.
Beispiele, welche Aufschluss zur Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Geometrische Reihen - Arithmetische Folgen - Geometrische Folgen - Arithmetische Reihe - Arithmetische Zahlenfolge - Geometrische Zahlenfolge - Konvergenz - Divergenz - Folgen - Reihen - Reihe plotten - Grafische Darstellung - Geometrische Summenformel - Differenzenfolge - Summenfolge - Partialsummen - Partialsummenfolge - Alternierende Folge - Differenzenfolgen - Summenfolgen - Partialsummenfolgen - Unendliche Reihen - Konvergente Reihe - Summe der Reihe - Summe einer Reihe - Definition - Teilfolge - d - s - n - sn - a1 - Explizit - Grenzwert - Bestimmen - Bestimmung - Partialsumme - Teilsumme - Summe - Reihendarstellung - Ln - e - Sinus - Cosinus - Logarithmus - Sin - Cos - Tan - Reihe - Folge - Supremum - Infimum - Obere und untere Schranke - Bildungsvorschrift - Bildungsgesetz - Explizites Bildungsgesetz - Quotient - Glied - Anzahl - Grenzwert einer Reihe - Konvergente Reihen - Divergente Reihe - Divergente Reihen - Summenwert - Einführung - Formel - Schreibweise - Plotten - Graph - Formeln - Begriff - Begriffe - Bilder - Beispiele - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Was ist - Was sind - Erklärung - Einfach erklärt - Bedeutung - Was bedeutet - Welche - Welcher - Welches - Wodurch - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Rechner - Berechnen - Eigenschaften - Darstellung - Tabelle - Gauß - Gaußsche Summenformel - Kleiner Gauß - Harmonische Reihe - Alternierende harmonische Reihe - Harmonische Folge - Teleskopreihe - Exponentialreihe - Logarithmische Reihe - Trigonometrische Reihe - Sinusreihe - Cosinusreihe - Eulersche Zahl - Logarithmus - Unendliche Reihen - Alternierende Reihe - Alternierende Reihen - Wert einer Reihe - Mathematische Folge - Mathematische Folgen - Mathematische Reihen - Erklärung - Beschreibung - Berechnung - Darstellen |
Arithmetische Zahlenfolgen - Geometrische Zahlenfolgen - Geometrische Reihen

Modul Arithmetische und geometrische Zahlenfolgen
Im Unterprogramm [Analysis] - [Zahlenfolgen] - Arithm. und geom. Zahlenfolgen können u.a. Untersuchungen mit arithmetischen und geometrischen Folgen, sowie geometrischen Reihen durchgeführt werden.

Abbildung 1 - Eingabefenster für arithmetische Zahlenfolgen

Abbildung 2 - Eingabefenster für geometrische Zahlenfolgen

Abbildung 3 - Eingabefenster für geometrische Reihen
Eine Folge wird als arithmetische Folge bezeichnet, wenn jedes Glied an für n ≥ 2 das arithmetische Mittel seiner Nachbarglieder ist. Eine Folge dieser Art liegt vor, wenn für alle aufeinander folgenden Glieder an+1−an = const gilt. Jedes Glied einer Folge dieser Art wird aus dem vorangegangenen Glied berechnet und ist somit rekursiv.
Eine arithmetische Reihe stellt die Summe einer Folge dar, in welcher jeder Term durch Addition (bzw. Subtraktion) einer Konstanten aus dem vorherigen berechnet wird.
Eine Folge wird als geometrische Folge bezeichnet, wenn der Quotient q zweier benachbarter Glieder konstant ist (wenn q ≠ 1). Es handelt sich um eine Zahlenfolge, bei welcher benachbarte Folgenglieder stets im gleichen Verhältnis zueinander stehen. Sie liegt vor, wenn für alle aufeinander folgende Glieder q = an+1/ an = const gilt.
Werden die Glieder einer geometrischen Folge addiert, so resultiert hieraus eine geometrische Reihe. Eine Reihe dieser Art stellt eine Zahlenfolge dar, bei welcher jedes einzelne Glied das Produkt des unmittelbar vorherig angeordneten Gliedes und einem konstanten Faktor ist.
In diesem Modul stehen zur Auswahl:
-
Berechnung und Darstellung der Glieder arithmetischer Folgen
-
Berechnung und Darstellung der Glieder geometrischer Folgen
-
Berechnung geometrischer Reihen
I - Arithmetische Zahlenfolgen

Arithmetische Folge - Formeln - Definition
Nachfolgend aufgeführt sind einige Formeln, welche zur Berechnung der Werte entsprechender Größen einer arithmetischen Zahlenfolge relevant sind.
Definition - Formel:
an = a1 + (n-1)·d
an+1 = an + d
Es gilt:
d < 0: Folge monoton fallend
d = 0: Folge konstant
d > 0: Folge monoton wachsend
Arithmetische Zahlenfolgen weisen eine konstante Differenzenfolge auf.
Partialsumme - Formel:
sn = n/2[2a1 + (n-1) d)] = n(a1 + an)/2
Verwendete Bezeichnungen:
| d: | Differenz zweier benachbarter Glieder |
| a1: | Anfangsglied einer Folge |
| an: | n-tes Glied einer Folge |
| n: | Anzahl der Glieder der Folge |
| sn: | n-te Partialsumme der ersten n Glieder |
| a(k): | Definitionsgleichung |
Gaußsche Summenformel (Kleiner Gauß)
Die Gaußsche Summenformel (kleiner Gauß) ist eine Formel für die Summe der ersten n aufeinanderfolgenden natürlichen Zahlen. Diese Reihe ist ein Spezialfall der arithmetischen Reihe. Sie lautet:
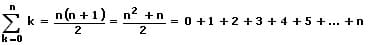
Hierbei erfolgt die Aufsummierung aller natürlicher Zahlen ausgehend von der Zahl 1 bis zur festgelegten Grenze n.
Arithmetische Folge - Berechnung und Darstellung
Um Berechnungen mit arithmetischen Zahlenfolgen durchführen und sich diese darstellen zu lassen, sollten Sie folgende Vorgehensweise anwenden:
- Wählen Sie das Registerblatt Arithmetische Zahlenfolge.
- Geben Sie die Werte von exakt 3 der 5 zur Verfügung stehenden Größen in die entsprechenden Felder ein.
- Um sich zusätzlich die Werte der ersten Glieder der Reihe in der Tabelle ausgeben zu lassen, aktivieren Sie das Kontrollkästchen Tabellenwerte ausgeben. Die Anzahl der Werte auszugebender Glieder kann im dafür vorgesehenen Eingabefeld festgelegt werden (voreingestellt: 100).
- Möchten Sie zudem das Ergebnis der Summation von Gliedern über einen bestimmten Wertebereich ermitteln lassen, so aktivieren Sie das Kontrollkästchen mit der Bezeichnung Partialsumme errechnen und geben die entsprechenden Werte in die Felder Partialsumme von und Partialsumme bis ein.
- Das Programm errechnet nach der Bedienung der Schaltfläche Berechnen die Werte der noch zu ermittelnden Größen, sowie die Definitionsgleichung a(k) der arithmetischen Zahlenfolge, und gibt diese in der oben angeordneten Tabelle aus.
- Soll die Folge grafisch ausgegeben werden, so bedienen Sie die Schaltfläche Darstellen.
- Benutzen Sie die aufklappbare Box Auswahl, um die Darstellungsart der Folge auszuwählen. Zur Verfügung stehen: Punkte, Punkte und Linien sowie Balken.
Hinweis:
Nicht für jeden Fall existieren eindeutige Lösungen. Insbesondere gibt es Fälle, bei welchen zwei Lösungen existieren. Tritt dies ein, so werden auch diese ausgegeben, wobei zu überprüfen bleibt, welche dieser eine eindeutige Lösung darstellt. Dies kann bei der Vorgabe der Größen a1, d und sn, wie auch bei der Vorgabe der Größen an, d, und sn eintreten.
II - Geometrische Zahlenfolgen

Geometrische Folge - Formeln - Definition
Nachfolgend aufgeführt sind einige Formeln, welche zur Berechnung der Werte entsprechender Größen einer geometrischen Zahlenfolge relevant sind.
Definition - Formeln:
an = a1 + qn-1
an+1 = an·q
an = √(an-1·an+1)
mit a1 ≠ 0 und q ≠ 0
Es gilt:
q < 0: Folge alternierend
0 < q < 1: Folge monoton fallend
q = 1: Folge konstant
q > 1: Folge monoton wachsend
Geometrische Zahlenfolgen weisen eine konstante Quotientenfolge auf. Sie sind konvergent für -1 < q ≤ 1 und divergent für q > 1 sowie q ≤ -1
Partialsumme - Formel:
mit q ≠ 1 gilt (geometrische Summenformel):

Folgende Kombinationen werden vom Programm analytisch gelöst:
a1-an-sn
a1-q-sn
a1-q-n
a1-q-an
a1-n-an
q-n-an
q-n-sn
Nachfolgend aufgeführte Kombinationen werden vom Programm numerisch iterativ gelöst:
n-an-sn
q-an-sn
a1-n-sn
Verwendete Bezeichnungen:
| q: | Quotient zweier benachbarter Glieder |
| a1: | Anfangsglied einer Folge |
| an: | n-tes Glied einer Folge |
| n: | Anzahl der Glieder der Folge |
| sn: | n-te Partialsumme der ersten n Glieder |
| a(k): | Definitionsgleichung |
Geometrische Folge - Berechnung und Darstellung
Um Berechnungen mit geometrischen Zahlenfolgen durchführen und diese grafisch auszugeben zu lassen, sollten Sie folgende Vorgehensweise anwenden:
- Wählen Sie das Registerblatt Geometrische Zahlenfolge.
- Geben Sie die Werte von exakt 3 der 5 zur Verfügung stehenden Größen in die entsprechenden Felder ein.
- Um sich zusätzlich die Werte der ersten Glieder der Reihe in der Tabelle ausgeben zu lassen, aktivieren Sie das Kontrollkästchen Tabellenwerte ausgeben. Die Anzahl der Werte auszugebender Glieder kann im dafür vorgesehenen Eingabefeld festgelegt werden (voreingestellt: 100).
- Möchten Sie zudem das Ergebnis der Summation von Gliedern über einen bestimmten Wertebereich ermitteln lassen, so aktivieren Sie das Kontrollkästchen mit der Bezeichnung Partialsumme errechnen und geben die entsprechenden Werte in die Felder Partialsumme von und Partialsumme bis ein.
- Das Programm errechnet nach der Bedienung der Schaltfläche Berechnen die Werte der noch zu ermittelnden Größen, sowie die Definitionsgleichung a(k) der geometrischen Zahlenfolge, und gibt diese in der oben angeordneten Tabelle aus.
- Soll die Folge grafisch ausgegeben werden, so bedienen Sie die Schaltfläche Darstellen.
- Benutzen Sie die aufklappbare Box Auswahl, um die Darstellungsart der Folge auszuwählen. Zur Verfügung stehen: Punkte, Punkte und Linien sowie Balken.
Hinweis:
Nicht für jeden Fall existieren eindeutige Lösungen. Dies trifft insbesondere auf iterativ zu lösende Aufgaben zu, jedoch können auch interne Rundungsfehler dazu führen, dass bei arithmetisch lösbaren Aufgaben keine Lösung gefunden wird. Bei Einteten einer solchen Situation wird eine entsprechende Meldung ausgegeben.
III - Reihen
Die Summe von Gliedern einer Folge wird als Reihe bezeichnet. Eine Reihe ist die Summe der Glieder einer unendlichen Zahlenfolge. Von einer Reihe wird gesprochen, wenn die Glieder einer Folge additiv miteinander verknüpft sind und somit eine Summe bilden. Eine Reihe wird auch als Summenfolge bezeichnet. Für sie gilt:
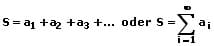
Endliche Reihen:
Als endliche Reihe wird eine Teilsummenfolge bezeichnet, bei der eine Beschränkung der Anzahl Ihrer Glieder vorliegt.
Unendliche Reihen:
Als unendliche Reihe wird eine Teilsummenfolge bezeichnet, bei der keine Beschränkung der Anzahl Ihrer Glieder vorliegt.
Konvergenz und Divergenz von Reihen:
Eine Reihe kann entweder konvergieren oder divergieren. Eine unendliche Reihe ist exakt dann konvergent, wenn ihre Partialsummenfolge konvergiert. Divergiert diese, so ist die Reihe divergent. Der Grenzwert S einer Partialsummenfolge heißt Summe der Reihe (Summe einer Reihe).
Die Konvergenz einer Reihe besagt, dass ihr Wert endlich ist. Für eine konvergente Reihe gilt:
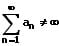
Die Divergenz einer Reihe besagt, dass ihr Wert unendlich ist. Für eine divergente Reihe gilt:
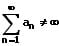
Alternierende Reihe:
Als alternierende Reihe wird eine unendliche Reihe bezeichnet, deren Glieder der zugehörigen Folge aus reellen Zahlen bestehen, welche wechselnde Vorzeichen besitzen.
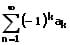
Harmonische Reihe - Harmonische Folge - Teleskopreihe
Als harmonische Folge wird die Zahlenfolge bezeichnet, welche sich aus den Kehrwerten der positiven ganzen Zahlen bildet.
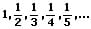
Ihre allgemeine Definition (das Bildungsgesetz) lautet:

Bei der harmonischen Folge besitzt jedes Glied den Wert des harmonischen Mittels seiner benachbarten Glieder. Die harmonische Reihe ist eine Reihe, welche aus der Summation der Glieder 1 + 1/2 + 1/3 + 1/4 .... der harmonischen Folge resultiert. Ihre Definition lautet:
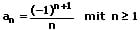
Bei einer Teleskopreihe handelt es sich um eine Reihe, bei welchen sich benachbarte Glieder gegenseitig aufheben. Als Teleskopsumme wird eine endliche Summe bezeichnet, bei welcher sich die Summe zweier benachbarter Glieder gegenseitig aufhebt. Summen dieser Art besitzen die Formen (Bildungsgesetze):
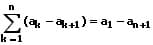
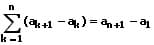
IV - Geometrische Reihen
Eine geometrische Reihe ist die Reihe einer geometrischen Folge. Ist der Betrag des Quotienten |q| einer geometrischen Reihe kleiner 1, so konvergiert sie. Ist |q| ≥ 1 (Grenzwert der Partialsummenfolge), so divergiert sie.
Geometrische Reihe - Formeln - Definition
Nachfolgend aufgeführt sind einige Formeln, welche zur Berechnung der Werte entsprechender Größen einer geometrischen Reihe relevant sind.
Definition - Formel:

konvergent für |q| < 1
Partialsumme:
sn = a1 / (1 - q)
Verwendete Bezeichnungen:
| a1: | Anfangsglied einer Folge |
| q: | Quotient zweier benachbarter Glieder |
| sn: | n-te Partialsumme der ersten n Glieder |
| n: | Anzahl der Glieder der Folge |
Geometrische Reihe - Berechnung
Um Berechnungen mit einer geometrischen Reihe durchführen zu lassen, führen Sie Folgendes aus:
- Wählen Sie das Registerblatt Geometrische Reihe.
- Geben Sie die Werte für a1 und q in die dafür vorgesehenen Felder ein.
- Bedienen Sie die Schaltfläche Berechnen, so wird das Ergebnis der Summe der geometrischen Reihe ausgegeben.
Hinweis:
Ist die definierte Reihe konvergent, so wird das Ergebnis angezeigt, andernfalls erhalten Sie eine Fehlermeldung.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung des entsprechenden Kontrollkästchens folgende zusätzliche Einstellung vornehmen:
- Beschriftung: Beschriftung dargestellter Punkte ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Rekursive Zahlenfolgen - Interaktiv
Beispiele - Aufgaben
Beispiel 1 - Arithmetische Zahlenfolgen:
Als bekannte Größen einer arithmetischen Zahlenfolge seien gegeben:
Glied a(1): 2
Glied a(n): 5
Anzahl n: 12
Es gilt die Differenz d sowie die Summe sn der Zahlenfolge ermitteln zu lassen.
Vorgehensweise und Lösung:
Nach einer Wahl des Registerblatts Arithmetische Zahlenfolgen, einer Eingabe der o.a. Werte in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen werden folgende Ergebnisse ausgegeben:
Differenz d: 0,272
Summe sn: 42
Ferner ermittelt das Programm für die Definitionsgleichung der Zahlenfolge den Term:
a(k) = 1,7272+0,2727·K
Beispiel 2 - Geometrische Zahlenfolgen:
Von einer geometrischen Zahlenfolge seien folgende bekannte Größen gegeben:
Glied a(1): 3
Glied a(n): 1
Anzahl n: 6
Es ist der Quotient q sowie die Summe sn der Zahlenfolge zu ermitteln.
Vorgehensweise und Lösung:
Wird das Registerblatt Geometrische Zahlenfolgen aktiviert und werden die zuvor aufgeführten Zahlenwerte in die dafür vorgesehenen Felder eingegeben, so gibt das Programm nach einer Bedienung der Schaltfläche Berechnen aus:
Quotient q: 0,802
Summe sn: 11,138
Ferner wird für die Definitionsgleichung der Zahlenfolge der nachfolgend aufgeführte Term angezeigt:
a(k) = 3·0,80274(K-1)
Beispiel 3 - Geometrische Reihe:
Einem Quadrat mit der Seitenlänge a = 1 ist ein zweites Quadrat derart eingeschrieben, dass dessen Eckpunkte die Seiten des ersten Quadrats im Verhältnis 1:2 teilen; dem zweiten Quadrat wird ein drittes Quadrat nach derselben Vorschrift eingeschrieben usw.
Vorgehensweise und Lösung:
Nach einer Wahl des Registerblatts Geometrische Reihe, einer Eingabe der Zahlenwerte für a = 1 und q = 0,5, sowie der Bedienung der Schaltfläche Berechnen erhalten Sie das Ergebnis:
Summe der geom. Reihe: 2
Es ergibt sich somit eine max. Gesamthöhe (als Summe der unendlichen Reihe) von 2 mit a = 1 und q = 1/2. Dies entspricht dem Grenzwert der unendlichen Reihe: 1 + 1/2 + 1/4 +1/8 +1/16 ... = 2.

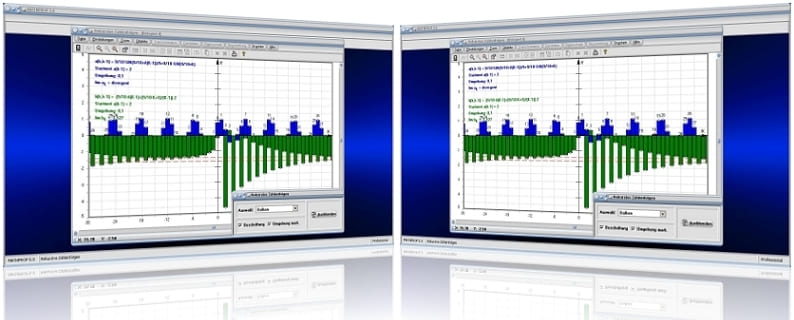
Grafische Darstellung - Arithmetische Zahlenfolge - Beispiel 1

Grafische Darstellung - Arithmetiscche Zahlenfolge - Beispiel 2

Grafische Darstellung - Geometrische Zahlenfolge - Beispiel 1

Grafische Darstellung - Geometrische Zahlenfolge - Beispiel 2
V - Arithmetische Reihen
Bei arithmetischen Reihen ist die Differenz zweier aufeinander folgender Glieder konstant. Der Summenwert einer Reihe ist das Resultat einer Addition. Ihr Summenwert errechnet sich wie nachfolgend gezeigt:
a + (a + d) + (a + 2d) + ... + [a + (n-1)d] = n/2 [2a + (n-1)d]
Mit:
a: Anfangsglied
a + (n-1)d: Endglied
k = 1, 2, 3, ... n
VI - Unendliche Reihen - Partialsummen
Eine Partialsumme (Teilsumme) sn wird aus den Gliedern einer unendlichen Zahlenfolge gebildet. Sie heißt n-te Partialsumme und ihre Definition sowie ihre Schreibweise lautet:
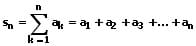
Die Folge dieser Partialsummen wird als unendliche Reihe bezeichnet. Sie ist wie folgt definiert:
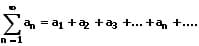
Besitzt diese Folge der Partialsummen sn einen Grenzwert s, so lautet ihre Bezeichnung konvergent mit dem Summenwert s.
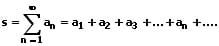
Besitzt sie hingegen keinen Summenwert, so heißt sie divergent.
VII - Spezielle und sonstige Reihen
Exponentialreihe - Logarithmische Reihe - Trigonometrische Reihe - Sinusreihe - Cosinusreihe - Reihendarstellung
Nachfolgend aufgeführt sind einige wichtige konvergente sowie spezielle Reihen (ln, e, ex, ax, ln x, sin x, cos x, tan x).
I - Wichtige konvergente Reihen:
Eulersche Zahl:

Natürlicher Logarithmus der Zahl 2:

Zahl 1:

II - Reihen für Exponentialfunktionen (Exponentialreihen):


III - Reihen für Logarithmusfunktionen (Logarithmische Reihen - Natürlicher Logarithmus):


IV - Reihen für trigonometrische Funktionen (Sinusreihe - Cosinusreihe - Tangensreihe):
Reihendarstellung - Sinus:

Reihendarstellung - Cosinus:

Reihendarstellung - Tangens:

Reihendarstellung - Cotangens:

Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Arithmetische Folge sowie unter Wikipedia - Geometrische Folge und unter Wikipedia - Infimum und Supremum zu finden.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
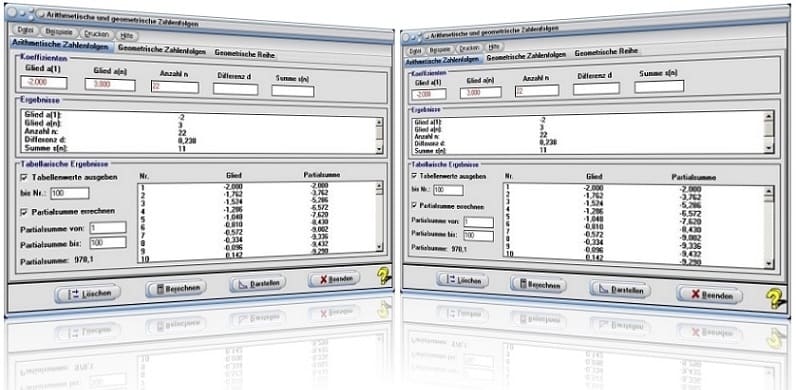
Startfenster des Unterprogramms Artihmetische und geometrische Zahlenfolgen
MathProf 5.0 - Unterprogramm Rekursive Zahlenfolgen

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.


















