MathProf - Annuitätenrechner - Ratentilgung - Annuitätendarlehen

       

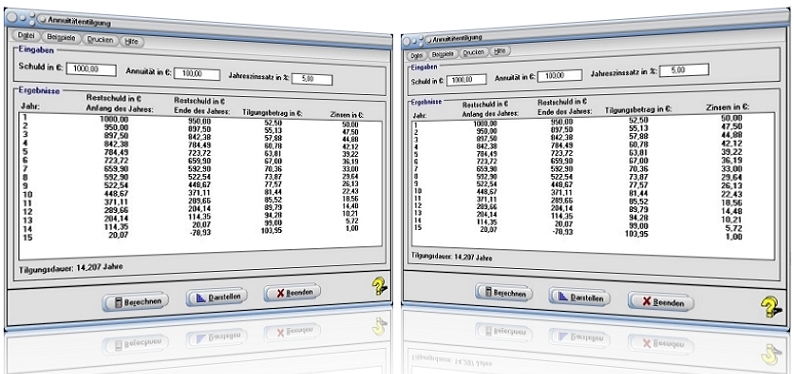
Modul Annuitätentilgung

---

 
Das Unterprogramm [Sonstiges] - Annuitätentilgung ermöglicht die Berechnung der Zinsen bei Annuitätentilgung (Ratentilgung nach der Annuitätenmethode) eines Darlehens.

 

 

 
Ein Annuitätendarlehen ist ein Darlehen mit konstanten Rückzahlungsbeträgen (Raten). Im Gegensatz zum Tilgungsdarlehen bleibt bei einer Annuitätentilgung die Höhe der zu zahlenden Rate über die gesamte Laufzeit gleich (sofern eine Zinsbindungsfrist über die gesamte Laufzeit vereinbart wurde). Annuitätentilgung führt dazu, dass sich der Zinsanteil der Rate monatlich zu Gunsten des Tilgungsanteils verändert.

Als Annuitäten werden die Jahreszahlungen bezeichnet, die Zins und Tilgung auf ein gewährtes Darlehen beinhalten. Die Annuitätenrate, oder kurz Annuität, setzt sich aus einem Zins- und einem Tilgungsanteil (einer Tilgungsrate) zusammen. Da mit jeder Rate ein Teil der Restschuld getilgt wird, verringert sich der Zinsanteil zugunsten des Tilgungsanteils. Erst gegen Ende der Kreditaufzeit ist eine deutliche Minderung der Schuld (Schulden) zu beobachten.
 
Die Tilgungsrechnung behandelt die Rückzahlung von Darlehen, Krediten und Hypotheken. Vom Schuldner wird erwartet, dass dieser seine Schuld dem Gläubiger binnen eines festgelegten Zeitraums (der Tilgungszeit oder Tilgungsdauer) verzinst und gemäß einem festgelegten Tilgungsplan zurückerstattet. Erfolgt die Rückzahlung (die Tilgung bzw. Schuldentilgung) des geliehenen Betrags in Teilbeträgen, so wird von einer Tilgungsschuld gesprochen.

Meist erfolgen die Tilgung des geliehenen Betrags und die Zinszahlung nachschüssig.

Die Tilgungsraten bei einer Annuitätentilgung stellen eine geometrisch wachsende Folge dar. Sie, sowie die zu erbringenden Zinszahlungen sind zu Beginn der Tilgung zunächst geringer und erhöhen sich mit zunehmender Dauer. Die verbleibenden Restschulden sind bei einer Annuitätentilgung grundsätzlich höher als bei Durchführung einer Ratentilgung.
 
Neben der Annuitätentilgung ist die Ratentilgung eine weitere Grundform der Rückzahlung eines Darlehens. Bei einer Ratentilgung sind die Tilgungen des Kreditnehmers im Gegensatz zur Annuitätentilgung regelmäßig und in gleicher Höhe zu tätigen.
 

Der in diesem Modul implementierte Tilgungsrechner (Annuitätenrechner bzw. Darlehensrechner) ermöglicht es, die monatlich zu zahlenden Tilgungsraten, die Tilgung sowie die Laufzeit eines Annuitätendarlehens berechnen zu lassen und den Verlauf der Tilgung grafisch darzustellen.
  

 
Nachfolgend aufgeführt sind die Formeln zur Durchführung von Berechnungen bzgl. der Annuität. Wenn eine Schuld S₀ nachschüssig über einen Zeitraum von n Jahren durch Annuitätentilgung bei einem Zinssatz p getilgt wird, so gilt:
 

Annuität:

 

 

Restschuld:

 

 

Tilgungsbetrag zum Zeitpunkt k:

 

 

Zinsbetrag zum Zeitpunkt k:

 

 

Vollständige Tilgungszeit:

 

 

T₁: Tilgung in erster Periode

n: Anzahl von Zinsperioden

A: Annuität

S₀: Anfangsschuld

S_n: Restschuld nach n Zinsperioden

p: Zinssatz

q: Aufzinsungsfaktor (q = 1+p/100)
 
 

 
Im folgenden sind Erläuterungen zu einigen Begriffen zu diesem Fachthema aufgeführt.

Amortisation: Mit dem Begriff Amortisation wird die allmähliche Tilgung einer Schuld beschrieben, die nach einem vorgegebenen Plan erfolgt.

Annuität: Als Annuität wird die jährlich regelmäßig fließende Zahlung an Zinsen und Tilgungsraten bezeichnet, die bei der Amortisation einer Schuld entrichtet wird. Sie beschreibt den Wert, den eine Investition erwartungsgemäß jährlich abwerfen wird. Wie bei vielen anderen dynamischen Investitionskalkulationen wird bei der Annuitätenmethode der Zeitwert des Geldes, und somit der Zeitpunkt der Zahlungen, einbezogen.

Tilgung: Unter dem Begriff Tilgung wird die Rückführung des Darlehens verstanden. Im Finanzwesen wird hiermit die planmäßige oder außerplanmäßige Rückzahlung von Schulden beschrieben.

Tilgungsplan: Als Tilgungsplan wird im Finanzwesen eine Liste künftiger Tilgungsbeträge bezeichnet, die in tabellarischer Form vorliegt. Sie umfasst die künftig zu entrichtenden Tilgungsbeträge sowie Kreditzinsen nebst zugehörigen Fälligkeiten.

Tilgungsanteil: Der Tilgungsanteil beschreibt den Anteil der Kreditrate, der für die Rückführung und somit für die Tilgung eines aufgenommenen Kreditbetrages aufzuwenden ist.

Annuitätenmethode: Als Annuitätenmethode wird ein klassische dynamisches Investitionsrechenverfahren bezeichnet, welches ein Bindeglied zum Rentenbarwert bildet. Der Kapitalwert einer Investition wird in diesem Fall auf die Nutzungsdauer in dem Maße verteilt, dass die Zahlungsfolge aus Einzahlungen und Auszahlungen in die Annuität umgewandelt wird. Hierbei erfolgt die Berechnung die Höhe der Zinsen oder der Rente bezogen auf eine Zeiteinheit.

Aufzinsung: Als Aufzinsung wird die Berechnung eines zukünftigen Werts bezeichnet, der die Zinsen und Zinseszinsen eines gegenwärtigen Betrags umfasst. Dieser zukünftige Wert wird Endwert genannt. Er wird mittels einer Methode berechnet, die unterschiedliche Zeitpunkte der Zahlungsströme berücksichtigt. Bei einer Aufzinsung werden somit nicht lediglich die anfallenden Zinseszinsen berechnet, sondern zudem die binnen eines Zeitraums angefallenen Zinsen.

Aufzinsungsfaktor: Der Aufzinsungsfaktor q erteilt Auskunft darüber, um welchen Faktor sich ein Kapital binnen einer Zinsperiode bei einem Zins von p vermehrt. Durch ihn erfolgt die Hochrechnung eines bestimmten Geldbetrags unter Berücksichtigung von Zins und Zinseszins auf einen nach einer bestimmten Anzahl von Zeiteinheiten fälligen Geldbetrag.

Tilgungsverlauf: Ein Tilgungsverlauf zeigt die Jahressummen monatlich zu zahlender Raten, bestehend aus Zins- und Tilgungszahlungen.

Tilgungsdarlehen: Der Begriff Tilgungsdarlehen ist der Oberbegriff für ein Darlehen, bei dem über eine feste Laufzeit eine Tilgungsleistung vereinbart wird.

Zinsfaktor: Der Zinsfaktor gibt an, um wie viel angelegtes Kapital binnen eines Zeitraums von einem Jahr wächst.

Restschuld: Mit dem Begriff Restschuld wird der Betrag beschrieben, der nach Abschluss eines Kredits noch ausstehend ist.

Schuldentilgungsdauer: Die Schuldentilgungsdauer gibt Auskunft darüber, nach wie vielen Jahren (binnen welchen Zeitraums) ein Kreditnehmer imstande wäre, seine noch ausstehenden Schulden zu bezahlen.

Amortisation (Amortisierung): Als Amortisation (Amortisierung) wird der Vorgang bezeichnet der durchzuführen ist, um einen Kredit über einen bestimmten, im Voraus festgelegten Zeitraum (die Amortisationszeit) zurückzuzahlen. Dieser Zeitraum wird Amortisationszeit oder Amortisationsdauer genannt.

 
Finanzmathematik: Die Finanzmathematik setzt sich unter anderem mit der Analyse von Finanzmärkten auseinander. Sie ist ein Zweig der angewandten Mathematik, die sich mit Themen aus den Bereichen von Finanzdienstleistern, wie etwa Banken oder Versicherungen, beschäftigt. Unter anderem behandelt sie finanzwirtschaftliche Themen wie z B. die Berechnung von Zinsen, Renten, Annuitäten, Tilgungen sowie Barwerten und Kapitalwerten.
 
 

 
Herr M. hat im Lotto einen Betrag in Höhe von 2.000.000 € gewonnen. Er möchte diesen Gewinn über einen Zeitraum von 10 Jahren verbrauchen. Wie hoch ist der Geldbetrag, den Herr M. jährlich ausgeben darf, um die gesamte Summe dieses Gewinns binnen des beschriebenen Zeitraums aufzubrauchen, wenn ihm die Bank einen Zinssatz von 3% gewährt?

Für die Annuität gilt wie oben gezeigt mit der Annuitätenformel. Diese lautet:

A = s₀ · qⁿ · (q-1) / (qⁿ-1)

Der Annuitätenfaktor rechnet sich mit:

A_f = qⁿ · (q-1) / (qⁿ-1)

Nach Einsetzen der entsprechenden Werte ergibt sich:

A_f = 1,03¹⁰ · (1,03-1) / ( 1,03¹⁰-1) = 0,11723

Somit beträgt der Annuitätenfaktor im vorliegenden Fall 0,11723.

Wird dieser Faktor mit dem Anfangswert s₀ (2.000.000 €) multipliziert, so ergibt sich:

2.000.000 · 0,11723 = 234.461,01 €

Herr M. kann somit innerhalb der nächsten 10 Jahre jährlich 234.461,01 € ausgeben, bis der Gewinn samt der resultierenden Zinsen aufgebraucht sein wird.
 

 

 

 
Nach Eingabe der Werte für Schuld, Annuität und Zinssatz in die dafür vorgesehenen Felder und einer Bedienung der Schaltfläche Berechnen werden die Ergebnisse in der Tabelle ausgegeben. Die zur Tilgung des Kredits erforderliche Zeit (Tilgungsdauer) wird unterhalb der Tabelle angezeigt.

 

Hinweis:

Bei Eingabe der Zahlenwerte ist darauf zu achten, dass die Annuität stets größer sein muss, als die anfallenden Zinsen (Schuld · Zinssatz), denn ansonsten ist keine Tilgung des Kredits möglich.

 

 
 

Möchten Sie sich die Zusammenhänge grafisch veranschaulichen, so bedienen Sie die Schaltfläche Darstellen.

Ausgegebene Diagramme können per Mausbedienung gezoomt werden.

Zoomen (Koordinatenwertebereich verkleinern)

Klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen Sie unter Festhalten der Taste ein Rechteck auf (von links nach rechts und von oben nach unten). Nach dem Loslassen der Maustaste wird der umrandete Bereich auf den Gesamtdarstellungsbereich vergrößert.

Urzustand

Möchten Sie den Koordinatenwertebereich wieder in den Urzustand versetzen, so klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen unter Festhalten der Taste ein Rechteck auf (von rechts nach links und von unten nach oben). Nach dem Loslassen der Maustaste wird der ursprüngliche Gesamtdarstellungsbereich wiederhergestellt.

Nach einer Bedienung der Schaltfläche Schließen kehren Sie wieder zum Hauptformular des Unterprogramms zurück.
 

 

Über den Menübefehl Datei - Ergebnisse exportieren besteht die Möglichkeit, die Ergebnisse in Tabellenform zu exportieren. Es stehen zur Verfügung:

 

Export in eine Excel-Tabelle im *.xls-Format (vertikale Anordnung)

Export in eine Excel-Tabelle im *.xls-Format (horizontale Anordnung)

Export in eine Text-Datei im *.txt-Format

Export in ein Word-Dokument im *.doc-Format in Tabellenform

Export in eine HTML-Seite im *.html-Format in Tabellenform

 

Achten Sie darauf, dass das entsprechende Programm (Word oder Excel) nicht geöffnet ist, während Sie diese Art von Datenexport durchführen, ansonsten erhalten Sie eine entsprechende Fehlermeldung.

 

Über den Menüpunkt Datei - Ergebnisse in Zwischenablage kopieren können die Ergebnisse in Tabellenform in die Zwischenablage kopiert werden. Nach dem Öffnen der entsprechenden Anwendung und einer Wahl des dortigen Befehls Einfügen bzw. der Bedienung der Tastenkombination Strg-V werden die Daten in der Anwendung abgelegt.
 
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs  (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Zinsrechnung

Jahreszinsrechnung

Zinseszinsrechnung grafisch

 

 

Es gilt, die Tilgungsdauer eines Kredits in Höhe von 10000 €, bei einer jährlichen Ratenzahlung von 2000 €, bei einem Jahreszinssatz von 8% ermitteln zu lassen.

 

Nach Eingabe des Werts 10000 in das Feld Schuld in €, der Eingabe des Werts 2000 in das Feld Annuität in € und der Festlegung der Zahl 8 im Feld Jahreszinssatz in %, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen unter anderem:

 

Zur Tilgung dieses Darlehens sind 6,637 Jahre erforderlich und zu Anfang des 7. Tilgungsjahres beträgt der noch zu tilgende Betrag 1196,89 €.

In einer Tabelle gibt das Programm für jedes Tilgungsjahr zudem aus:

- Restschuld zu Anfang des Jahres
- Restschuld am Ende des Jahres
- Zu leistender Tilgungsbetrag (jahresbezogen)
- Zinsen (jahresbezogen)
 

 

Beispiel 1


Beispiel 2


Beispiel 3


Beispiel 4

   
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
  

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Annuitätendarlehen zu finden.

 

 

Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach

 

MathProf 5.0 - Unterprogramm Zinsrechnung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---