MathProf - Analyse impliziter Funktionen - Graph plotter - 3D

 

Modul Analyse implizit definierter Funktionen

---

 
Das Unterprogramm [3D-Mathematik] - Analyse implizit definierter Funktionen im Raum ermöglicht die grafische Untersuchung funktionaler Zusammenhänge, die in impliziter Form gegeben sind.

 

Mathematische Funktionen können nicht nur in expliziter, sondern auch in impliziter Form definiert werden. Die Untersuchung von Funktionen, die in der Form f(x,y) ≥ w, f(x,y) ≤ w bzw. f(x,y) = w vorliegen, gestaltet sich meist schwierig. Es besteht jedoch die Möglichkeit, Funktionen dieser Art als einen Sonderfall dreidimensionaler Funktionen der Form z = f(x,y) zu betrachten und diese nur an Punkten darzustellen, bei welchen deren Funktionswerte den Bedingungen z ≥ w, z ≤ w bzw. z = w genügen. Werden die Konturverläufe (Randlinien) dieser, parallel zur (x,y)-Ebene liegenden Punktmengen betrachtet, so lässt sich der Funktionsverlauf der entsprechenden Kurve ableiten.

 

In diesem Modul wird es ermöglicht, Untersuchungen dieser Art durchzuführen. Es besteht die Möglichkeit, Zusammenhänge dieser Art grafisch, sowohl ohne, wie auch unter dem Einfluss von Funktionsparametern zu untersuchen. Das Modul ermöglicht eine Darstellung von Flächen und Punktmengen, die beschrieben werden durch
 

• Implizit definierte Funktionen der Formen:
  
  z = f(x,y,p) ³ w 
  z = f(x,y,p) ≥ w
  z = f(x,y,p) = w

Hierbei kann sowohl die Fläche ausgegeben werden, die durch eine Funktion der Form z = f(x,y) beschrieben wird (explizit), wie auch die Punktmenge einer Ebene die Bedingungen der Art z ≥ w, z ≤ w bzw. z = w erfüllt (implizit). Parameter w ist ein frei wählbarer, reeller Zahlenwert.
 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

 

Um Untersuchungen mit implizit definierten Funktionen dieser Art durchzuführen, sollten Sie Folgendes ausführen:
 

1. Definieren Sie den Funktionsterm im Eingabefeld mit der Bezeichnung z = f(x,y,p) = und beachten Sie hierbei die geltenden Syntaxregeln. 
    
2. Bestimmen Sie durch die Aktivierung des Kontrollschalters z = f(x,y,p) >= w, z = f(x,y,p) <= w bzw. z = f(x,y,p) = w die Art der zu erfüllenden Bedingung und geben Sie den entsprechenden Zahlenwert für w in das dafür vorgesehene Feld ein.
    
3. Wählen Sie durch die Aktivierung des Kontrollschalters Automatisch bzw. Statisch, ob das Programm den Z-Koordinatenwertebereich (vertik. Darstellungsbereich) automatisch bestimmen soll, oder ob Sie diesen vorgeben möchten. Trifft Letzteres zu, so legen Sie diesen durch die Eingabe eines entsprechenden Zahlenwerts in das Feld Darstellungsbereich Z fest.
    
4. Legen Sie ggf. durch die Eingabe entsprechender Zahlenwerte in die Felder Darstellungsbereich X sowie Darstellungsbereich Y die (x,y)-Darstellungsbereiche fest, über welche die Fläche ausgegeben werden soll.
    
5. Enthält der Funktionsterm das Einzelzeichen P, so führen Sie Folgendes durch:
   
   Definieren Sie, durch die Eingabe von Zahlenwerten in die Felder Parameter p von ... und bis ..., den Startwert, sowie den Endwert des vom Parameter P zu durchlaufenden Wertebereichs und legen Sie durch die Eingabe eines entsprechenden Werts in das Feld Schrittweite die Schrittweite für Parameter P fest. Voreingestellt sind der Startwert -5, der Endwert 5, sowie eine Schrittweite von 0,1.
   
   Wählen Sie durch die Aktivierung des Kontrollschalters Automatisch bei Simulation oder Manuell, ob Sie die Parameterwertsimulation manuell durchführen möchten, oder ob das Programm diese automatisch ausführen soll.
    
6. Bedienen Sie hierauf die Schaltfläche Darstellen.
    

Hinweise:

Werden Untersuchungen mit Funktionen durchgeführt, die nicht das Einzelzeichen P enthalten (parameterfreie Funktionen), so ist die Schaltfläche Sim. Start stets deaktiviert. Wurde hingegen eine Funktion definiert, welche dieses Zeichen enthält, und wurde die Durchführung einer manuellen Simulation gewählt, so steht auf dem Bedienformular ein Schieberegler P zur Verfügung, mit welchem Sie den zu verwendenden Wert für Parameter P einstellen können. Wurde eine automatische Simulation gewählt, so können Sie diese starten, indem Sie die Schaltfläche Start Sim. bedienen. Sie trägt hierauf die Bezeichnung Stop Sim. Beendet werden kann die Simulation wieder, indem Sie diese Schaltfläche nochmals bedienen. Es wird stets der Parameterwertebereich durchlaufen, welcher auf dem Hauptformular des Unterprogramms festgelegt wurde.

 

Bei Ausgabe der Darstellung kann durch die Aktivierung des Kontrollkästchens f(x,y,p) auf dem Bedienformular gewählt werden, ob die in expliziter Form definierte Fläche f(x,y,p) eingeblendet werden soll.

 

 

Zudem wird die Durchführung numerischer Analysen derartiger Zusammenhänge ermöglicht.

 

 

Wird der Menüpunkt Werte gewählt, so ermittelt das Programm für Punkte innerhalb eines frei wählbaren Areals der (x,y)-Ebene, ob die vorgegebene Bedingung erfüllt wird, oder nicht. Wird sie erfüllt, so wird dies in den entsprechenden Tabelleneinträgen angezeigt, andernfalls werden die z-Koordinatenwerte der Flächenfunktion ausgegeben. Um sich die numerisch ermittelten Berechnungsergebnisse ausgeben zu lassen, sollten Sie wie nachfolgend geschildert vorgehen:
 

1. Definieren Sie den Funktionsterm im Eingabefeld mit der Bezeichnung z = f(x,y) und beachten Sie hierbei die geltenden Syntaxregeln.
    
2. Bestimmen Sie, durch die Aktivierung des Kontrollschalters z = f(x,y) >= w bzw. z = f(x,y) <= w die Art der zu erfüllenden Bedingung und geben Sie den entsprechenden Zahlenwert für w in das dafür vorgesehene Feld ein.
    
3. Legen Sie durch die Eingabe entsprechender Werte in die Felder Von x1 =, bis x2 =, Von y1 = und bis y2 = den Bereich fest, über welchen Werte ausgegeben werden sollen.
    
4. Wählen Sie über die aufklappbare Auswahlbox die Schrittweite, mit welcher die Berechnungen durchzuführen sind (voreingestellt: 0,1).
    
5. Bedienen Sie die Schaltfläche Berechnen, so ermittelt das Programm die Ergebnisse und gibt diese in der Tabelle aus.

Es gilt zu achten, dass deklarierte Funktionsterme nicht das Einzelzeichen P enthalten, welches ausschließlich bei der Definition einer Funktion zur grafischen Darstellung Verwendung findet.

 

Hinweis:

Befindet sich im Eingabefeld des Hauptformulars des Unterprogramms bereits eine Funktionsdeklaration, so wird diese in das Eingabefeld des Unterformulars übernommen.

 

 

Den Bereich bzgl. der x- und y-Achse, der zur Ausgabe der grafischen Darstellung verwendet werden soll, legen Sie durch die Eingabe entsprechender Werte in die Felder Darstellungsbereich X und Darstellungsbereich Y im Formularbereich Darstellung - Voreinstellung Darstellungsbereiche für X und Y fest. Das Programm benutzt diese Werte um die räumliche Dimensionierung der Darstellung in x- wie in y-Achsrichtung festzulegen.

 

Bei der Darstellung ermöglicht das Programm die Bemessung des Z Darstellungsbereichs auf eine der folgenden Arten und Weisen:
 

• Automatisch

• Statisch

1. Automatisch:
   Wird die Einstellung Automatisch, durch die Aktivierung des entsprechenden Kontrollschalters gewählt, so ermittelt das Programm den zur vollständigen Darstellung der Fläche (Punktmenge) erforderlichen z-Koordinatenwert automatisch.

    

   Um Änderungen dieser Einstellungen bei der Ausgabe der grafischen Darstellung vorzunehmen, steht auf dem Bedienformular der Schalter Bereich zur Verfügung.

   Bedienen Sie diesen und legen Sie im hierauf erscheinenden Eingabeformular die Abmaße des gewünschten räumlichen Darstellungsbereichs bezüglich der x- und der y-Achse, durch die Eingabe entsprechender Werte in die Felder mit den Bezeichnungen Für x und Für y fest.

    

   Temporär kann die Bemessung des z-Darstellungsbereichs geändert (vergrößert) werden. Hierzu ist die Eingabe eines entsprechenden Werts notwendig. Dieser darf nicht unter dem vom Programm (im Eingabefeld) vorgegebenen Mindestwert liegen und wird nur bis zur erstmaligen Beendigung der Ausgabe der Darstellung beibehalten. Nach einer Bedienung der Schaltfläche Ok wird die Darstellung aktualisiert.
    

2. Statisch:

   Bei einer Aktivierung des Kontrollschalters Statisch stellt das Programm die Fläche (Punktmenge) innerhalb des gewählten z-Darstellungsbereichs dar und beschneidet diese an Stellen, die außerhalb dessen liegen. Diesen Bereich können Sie bei der Ausgabe der Darstellung verändern, indem Sie den, auf dem Bedienformular zur Verfügung stehenden, Rollbalken Z-Koord. positionieren. Der maximal einstellbare Wert entspricht dem Doppelten des unter Darstellungsbereich Z, auf dem Hauptformular des Unterprogramms vorgegebenen Werts.

    

   Um Änderungen dieser Einstellungen bei Ausgabe der grafischen Darstellung vorzunehmen, steht auf dem Bedienformular der Schalter Bereich zur Verfügung. Legen Sie im hierauf erscheinenden Eingabeformular die Abmaße des gewünschten räumlichen Darstellungsbereichs, durch die Eingabe der entsprechenden Werte in die Felder mit den Bezeichnungen Für x, Für y und Für z fest und bedienen Sie hierauf die Schaltfläche Ok.

 

Um die Anzeige der Funktionsbibliothek ein- bzw. auszublenden steht der Menüpunkt Option - Funktionsbibliothek ausblenden bzw. Option - Funktionsbibliothek einblenden zur Verfügung. Diese Einstellung wird sitzungsübergreifend gespeichert.

 

 

Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.

 

 

Flächen mit Funktionen in expliziter Form (3D)

 

 

Es gilt, sich die Lösungen einer implizit definierten Gleichung z = f(x,y) = x²/2 +y²/2 -1 mit der Bedingung z ≥ -0,2 als Punktmenge im dreidimensionalen Raum darstellen zu lassen.

 

Hierzu definieren Sie den Funktionsterm X^2/2+Y^2/2-1 im Eingabefeld z = f(x,y,p) =, geben den Zahlenwert -0,2 in das dafür vorgesehene Feld ein, aktivieren den Kontrollschalter z = f(x,y,p) >= w, belassen die Werte in den Formularbereichen Voreinstellung - Darstellungsbereiche auf den Vorgabeeinstellungen, wählen den Kontrollschalter Statisch und bedienen die Schaltfläche Darstellen.

 

Aktivieren Sie bei Ausgabe der grafischen Darstellung auf dem Bedienformular das Kontrollkästchen f(x,y,p), so wird zudem die Fläche ausgegeben, welche durch die definierte Funktion beschrieben wird (ohne die Berücksichtigung der gestellten Bedingung).

 

Um sich die Lösung einer Gleichung mit der Bedingung x²/2 +y²/2 -1 ≤ -0,2 als Punktmenge im dreidimensionalen Raum darstellen zu lassen, verwenden Sie zuvor durchgeführte Einstellungen, aktivieren den Kontrollschalter z = f(x,y,p) >= w auf dem Hauptformular des Unterprogramms und bedienen hierauf die Schaltfläche Darstellen.

 

Wird Kontrollschalter z = f(x,y,p) >= w auf dem Hauptformular des Unterprogramms aktiviert, so wird lediglich der Konturverlauf der parallel zur (x,y)-Ebene liegenden Punktmenge betrachtet, welche die Bedingung x²/2 +y²/2 -1 = -0,2 erfüllen. Diese wird als Linienkontur dargestellt.
 

 

Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7


Grafische Darstellung - Beispiel 8


Grafische Darstellung - Beispiel 9


Grafische Darstellung - Beispiel 10

   
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Flächen im Raum zu finden.

 

 

Rotation von Kurven in kartesischer Form um die X-Achse (3D) - Rotation von Kurven in Parameterform um die X-Achse (3D) - Rotation von Kurven in kartesischer Form um die Y-Achse (3D) - Rotation von Kurven in Parameterform um die Y-Achse (3D) - Flächen mit Funktion in expliziter Form (3D) - Flächen mit Funktionen in Parameterform (3D) - Funktionen in sphärischen Kugelkoordinaten (3D) - Funktionen in sphärischen Zylinderkoordinaten (3D) - Raumkurven in Parameterform (3D) - Flächen 2. Ordnung (3D)
 

 

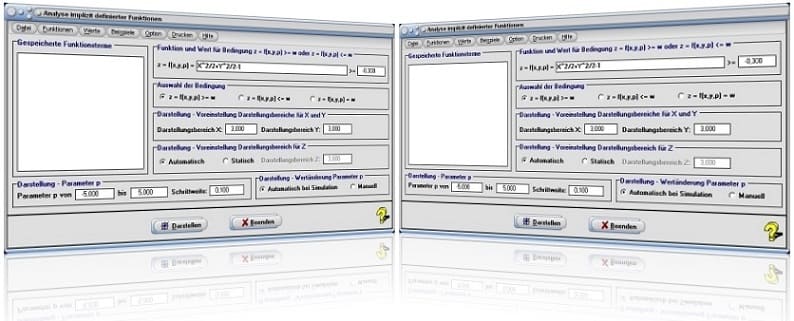
Startfenster des Unterprogramms Analyse implizit definierter Funktionen im Raum
 

MathProf 5.0 - Startfenster des Unterprogramms Flächen im Raum mit Funktionen in Parameterform

---

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---